khối lượng công việc tăng 32% . Hỏi phải tăng số người lao động thêm bao nhiêu % để năng suất lao động tăng 10%
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(mx+7=6\) (1) (m ≠ 0)
\(\Leftrightarrow mx=-1\)
\(\Leftrightarrow x=\frac{-1}{m}\)
Lại có: \(\frac{x}{2}+m=1\) (2)
\(\Leftrightarrow \frac{x}{2}=1-m\)
\(\Leftrightarrow x=2-2m\)
Để 2 phương trình (1) và (2) có nghiệm bằng nhau thì:
\(\frac{-1}{m}=2-2m\\\Leftrightarrow2m-2-\frac{1}{m}=0\\\Leftrightarrow 2m^2-2m-1=0(\text{vì }m\ne0)\\\Leftrightarrow \left[\begin{array}{} m=\frac{1+\sqrt3}{2}(tmdk)\\ m=\frac{1-\sqrt3}{2}(tmdk) \end{array} \right. \)
$\text{#}Toru$
Ta có pt(1):
\(mx+7=6\left(m\ne0\right)\)
\(\Leftrightarrow mx=6-7=-1\)
\(\Leftrightarrow x=-\dfrac{1}{m}\)
Pt(2) \(\dfrac{x}{2}+m=1\)
\(\Leftrightarrow\dfrac{x}{2}=1-m\)
\(\Leftrightarrow x=2\left(1-m\right)=2-2m\)
Vì 2 phương trình có nghiệm bằng nhau nên:
\(-\dfrac{1}{m}=2-2m\)
\(\Leftrightarrow-1=m\left(2-2m\right)\)
\(\Leftrightarrow-1=2m-2m^2\)
\(\Leftrightarrow2m^2-2m-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{3}}{2}\\m=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\left(tm\right)\)
Vậy: ...

Ta có pt(1): \(mx+7=6\left(m\ne0\right)\)
\(\Leftrightarrow mx=6-7\)
\(\Leftrightarrow mx=-1\)
\(\Leftrightarrow x=-\dfrac{1}{m}\)
pt(2): \(\dfrac{x}{2+m}=1\left(m\ne-2\right)\)
\(\Leftrightarrow x=1\cdot\left(2+m\right)=m+2\)
Vì 2 pt có 2 nghiệm bằng nhau nên ta có:
\(-\dfrac{1}{m}=m+2\)
\(\Leftrightarrow-1=m\left(m+2\right)\)
\(\Leftrightarrow-1=m^2+2m\)
\(\Leftrightarrow m^2+2m+1=0\)
\(\Leftrightarrow\left(m+1\right)^2=0\)
\(\Leftrightarrow m+1=0\)
\(\Leftrightarrow m=-1\left(tm\right)\)
Vậy: ...

Xét S là tổng của nghịch đảo tất cả các số trên bảng.
Do \(c=\dfrac{a\times b}{a+b}\) nên \(\dfrac{1}{c}=\dfrac{a+b}{a\times b}=\dfrac{1}{a}+\dfrac{1}{b}\)
Vì vậy, khi xóa 2 số \(a,b\) và thay bằng số c thì S không đổi.
Khi đó, nếu số còn lại trên bảng là \(x\) thì \(\dfrac{1}{x}=\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{9}\) \(=\dfrac{7129}{2520}\) hay \(x=\dfrac{2520}{7129}\)
Vậy số còn lại trên bảng là \(\dfrac{2520}{7129}\)

f; (\(x\) + 4).(\(x-2\)) = 0
\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-4; 2}
g; (\(x\) - 2).(\(x\) + 3) < 0
\(x\) - 2 = 0 ⇒ \(x\) = 2; \(x\) + 3 = 0 ⇒ \(x\) = -3
Lập bảng ta có:
| \(x\) | - 3 2 |
| \(x-2\) | - - 0 + |
| \(x\) + 3 | - 0 + + |
| (\(x-2\)).(\(x+3\)) | + 0 - 0 + |
Theo bảng trên ta có -3 < \(x\) < 2
Vậy -3 < \(x\) < 2

a) Vì \(p\) là snt lớn hơn 3 nên \(p⋮̸3\) \(\Rightarrow p^2\equiv1\left[3\right]\) hay \(p^2-1⋮3\)
b) Theo câu a), ta có \(p^2\equiv q^2\equiv1\left[3\right]\) nên \(p^2-q^2⋮3\)
c) Vì \(p,q\) là các snt lớn hơn 3 nên chúng cũng là các snt lẻ \(\Rightarrow p^2\equiv q^2\equiv1\left[8\right]\)
\(\Rightarrow p^2-q^2⋮8\)

Cho \(p=2,p=3\) ta thấy không thỏa mãn.
Cho \(p=5\) ta thấy thỏa mãn.
Xét \(p>5\), khi đó \(p⋮̸5\). Khi đó \(p^2\equiv1,4\left[5\right]\) (tính chất của scp)
Khi \(p^2\equiv1\left[5\right]\) thì \(p^2+1⋮5\), khi \(p^2\equiv4\left[5\right]\) thì \(p^2+6⋮5\) nên 1 trong 2 số này là hợp số, không thỏa mãn.
Vậy \(p=5\) là snt duy nhất thỏa mãn ycbt.
Đây là dạng toán nâng cao chuyên đề số nguyên tố, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau.
+ Nếu p = 2 ta có: p2 + 4 = 22 + 4 = 4 + 4 = 8 (loại)
+ Nếu p = 3 ta có: p2 + 6 = 32 + 6 = 9 + 6 = 15 (loại)
+ Nếu p = 5 ta có: p2 + 4 = 52 + 4 = 25 + 4 = 29 (thỏa mãn)
p2 + 6 = 52 + 6 = 25 + 6 = 31 (thỏa mãn)
+ Nếu p > 5 khi đó: p2 : 5 dư 1 hoặc 4 (tính chất số chính phương)
TH1 p2 : 5 dư 1 ⇒ p2 + 4 ⋮ 5 (là hợp số loại)
TH2 p2 : 5 dư 4 \(\Rightarrow\) p2 + 6 ⋮ 5 (là hợp số loại)
Từ những lập luận trên ta có:
p = 5 là giá trị số nguyên tố duy nhất thỏa mãn đề bài
Kết luận số nguyên tố thỏa mãn đề bài là 5.

e) \(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy: ...
f) \(\left(x+4\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy: ...
g) \(\left(x-2\right)\left(x+3\right)< 0\)
TH1: \(\left\{{}\begin{matrix}x-2>0\\x+3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\)
\(\Rightarrow x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-2< 0\\x+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2\\x>-3\end{matrix}\right.\)
\(\Rightarrow-3< x< 2\)
Vậy: ...
h) \(\left(x-1\right)\left(x+2\right)>0\)
TH1: \(\left\{{}\begin{matrix}x-1>0\\x+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>1\\x>-2\end{matrix}\right.\)
\(\Rightarrow x>1\)
TH2: \(\left\{{}\begin{matrix}x-1< 0\\x+2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 1\\x< -2\end{matrix}\right.\)
\(\Rightarrow x< -2\)
Vậy: ...
a) \(3\left(2x+7\right)-2x=9\Leftrightarrow6x+21-2x=9\)
\(\Leftrightarrow4x+21=9\)
\(\Leftrightarrow4x=9-21=-12\)
\(\Leftrightarrow x=\dfrac{-12}{4}=-3\)
Vậy: ...
b) \(\left[\left(7x-4\right):2-2\right]\cdot13=221\)
\(\Leftrightarrow\left(7x-4\right):2-2=\dfrac{221}{13}=17\)
\(\Leftrightarrow\left(7x-4\right):2=17+2\)
\(\Leftrightarrow\left(7x-4\right):2=19\)
\(\Leftrightarrow7x-4=19\cdot2=38\)
\(\Leftrightarrow7x=42\)
\(\Leftrightarrow x=\dfrac{42}{7}=6\)
Vậy: ...
c) \(x^2-9=0\)
\(\Leftrightarrow x^2=9\)
\(\Leftrightarrow x=\pm\sqrt{9}\)
\(\Leftrightarrow x=\pm3\)
Vậy: ....
d) \(5< x^2< 16\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2>5\\x^2< 16\end{matrix}\right.\)
Với \(x^2>5\Rightarrow\left[{}\begin{matrix}x< -\sqrt{5}\\x>\sqrt{5}\end{matrix}\right.\) (1)
Với \(x^2< 16\Rightarrow-4< x< 4\) (2)
Từ (1) và (2) \(\left[{}\begin{matrix}-4< x< -\sqrt{5}\\\sqrt{5}< x< 4\end{matrix}\right.\)
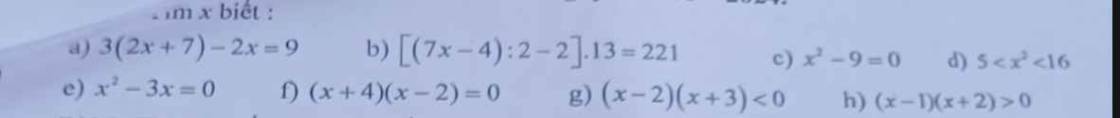
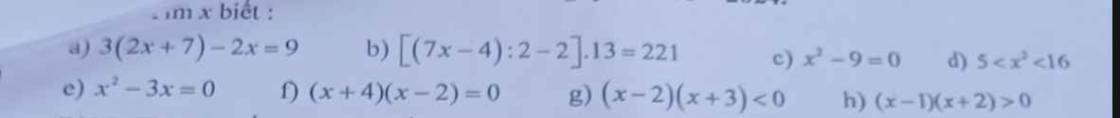
Coi khối lượng công việc là 100%
Năng xuất lao dộng là 100%
Khối lượng cộng việc mới bằng số phần trăm khối lượng công việc cũ là : 100%+32%=132%
Năng xuất lao động mới bằng số phần trăm năng xuất lao động cũ là :100%+10%=110%
Số người lao động mới bằng số phần trăm người lao động cũ là :
132%:110%=120%
Phải tăng số phần trăm là :
120%-100%=20%