Số bạn chỉ giỏi toán, chỉ giỏi tiếng việt hoặc giỏi cả 2 môn: 40 - 11 = 29 (học sinh)

Số học sinh giỏi cả 2 môn toán và tiếng việt: (23 + 18) - 29 = 12 (học sinh)

Đ.số:....

Số bạn chỉ giỏi toán, chỉ giỏi tiếng việt hoặc giỏi cả 2 môn: 40 - 11 = 29 (học sinh)

Số học sinh giỏi cả 2 môn toán và tiếng việt: (23 + 18) - 29 = 12 (học sinh)

Đ.số:....

Gọi số cần tìm là \(abc4\).

Theo bài: \(abc4+2187=4abc\)

\(\Rightarrow10\cdot abc+4+2187=4000+abc\)

\(\Rightarrow9abc=1809\Rightarrow abc=201\)

Vậy số tự nhiên cần tìm là \(2014\)

Gọi số cần tìm là 
�
�
�
4
abc4.

Theo bài: 
�
�
�
4
+
2187
=
4
�
�
�
abc4+2187=4abc

⇒
10
⋅
�
�
�
+
4
+
2187
=
4000
+
�
�
�
⇒10⋅abc+4+2187=4000+abc

⇒
9
�
�
�
=
1809
⇒
�
�
�
=
201
⇒9abc=1809⇒abc=201

Vậy số tự nhiên cần tìm là 
2014
 

68

12+56=68

  Vì viết nhầm dấu phẩy của một số thập phân sang trái một hàng nên số thập phân ban đầu gấp số thập phân lúc sau 10 lần

  Khi giữ nguyên một số hạng và giảm số hạng còn lại xuống 10 lần thì tổng mới kém tổng cũ là:

         10 - 1 = 9 (lần số lúc sau khi giảm)

  Tổng cũ hơn tổng mới là:

         149,96 - 36,047 = 113,913

   Số thập phân ban đầu khi chưa viết nhầm dấu phẩy là:

         113,913 :  9 x 10 = 126,57

   Số thập phân còn lại là:

       149,96 - 126,57 = 23,39

Đáp số:....

  Vì viết nhầm dấu phẩy của một số thập phân sang trái một hàng nên số thập phân ban đầu gấp số thập phân lúc sau 10 lần

  Khi giữ nguyên một số hạng và giảm số hạng còn lại xuống 10 lần thì tổng mới kém tổng cũ là:

         10 - 1 = 9 (lần số lúc sau khi giảm)

  Tổng cũ hơn tổng mới là:

         149,96 - 36,047 = 113,913

   Số thập phân ban đầu khi chưa viết nhầm dấu phẩy là:

         113,913 :  9 x 10 = 126,57

   Số thập phân còn lại là:

       149,96 - 126,57 = 23,39

???

2 số cần tìm là : 642 và 531 hoặc 631 hoặc 542 hoặc 632 và 541

Tổng các số trên đều không đổi và bằng 1173

???

??????????????????????????????????

Nửa chu vi mảnh đất là:

\(18:2=9\left(m\right)\)

Chiều dài mảnh đất là:

\(9\times5:\left(5+4\right)=5\left(m\right)\)

Chiều rộng mảnh đất là:

\(9\times4:\left(5+4\right)=4\left(m\right)\)

Diện tích mảnh đất là:

\(5\times4=20\left(m^2\right)\)

Diện tích trồng rau là:

\(20\times40\%=8\left(m^2\right)\)

Diện tích còn lại là:

\(20-8=12\left(m^2\right)\)

........

\(2^x-6^x-3^{x+1}+3=0\)

\(\Leftrightarrow2^x\left(1-3^x\right)+3\left(1-3^x\right)=0\)

\(\Leftrightarrow\left(2^x+3\right)\left(1-3^x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2^x+3=0\left(\text{vô nghiệm}\right)\\1-3^x=0\end{matrix}\right.\) 

\(\Rightarrow3^x=1\Rightarrow x=0\)

Để giải phương trình 2�−6�−3�+1+3=02x−6x−3x+1+3=0, trước hết hãy viết lại phương trình theo thứ tự các thành phần của �x:

2�−6�−3�+1+3=02x−6x−3x+1+3=0

Kết hợp các thành phần có cùng �x:

(−6�−3�−�)+(2+1+3)=0(−6x−3x−x)+(2+1+3)=0

−10�+6=0−10x+6=0

Bây giờ, để tìm giá trị của �x, hãy giải phương trình:

−10�+6=0−10x+6=0

Đưa hằng số về phía bên kia của phương trình:

−10�=−6−10x=−6

Giải phương trình để tìm giá trị của �x:

�=−6−10x=−10−6​

�=35x=53​

Vậy giá trị của �x là 3553​.

Để giải phương trình 2�−6�−3�+1+3=02x−6x−3x+1+3=0, trước hết hãy viết lại phương trình theo thứ tự các thành phần của �x:

2�−6�−3�+1+3=02x−6x−3x+1+3=0

Kết hợp các thành phần có cùng �x:

(−6�−3�−�)+(2+1+3)=0(−6x−3x−x)+(2+1+3)=0

−10�+6=0−10x+6=0

Bây giờ, để tìm giá trị của �x, hãy giải phương trình:

−10�+6=0−10x+6=0

Đưa hằng số về phía bên kia của phương trình:

−10�=−6−10x=−6

Giải phương trình để tìm giá trị của �x:

�=−6−10x=−10−6​

�=35x=53​

Vậy giá trị của �x là 3553​.

a) y x 5 = 1948 + 247

y x 5 = 2195

y = 2195 : 5

y = 439

b) y : 3 = 190 - 90

y : 3 = 100

y = 100 x 3

y = 300

c) y - 8357 = 3829 x 2

y - 8357 = 7658

y = 7658 + 8357

y = 16 015

d) y x 8 = 182 x 4

y x 8 = 728

y = 728 : 8

y = 91

a) y x 5 = 1948 + 247

y x 5 = 2195

y = 2195 :5

y = 439

b) y : 3 = 190 - 90

y : 3 = 100

y = 100 x 3

y = 300

c) y - 8357 = 3829 x 2

y - 8357 = 7658

y = 7658 + 8357

y = 16015

d) y x 8 = 182 x 4

y x 8 = 728

y = 728 : 8

y = 91

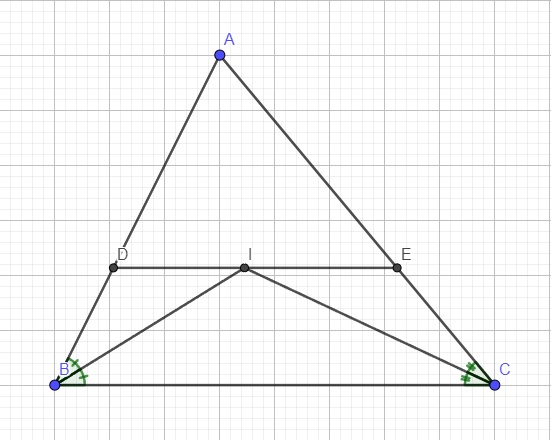
a,

Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang

Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang

Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang

b.

Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)

Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)

\(\Rightarrow\widehat{DBI}=\widehat{BID}\)

\(\Rightarrow\Delta BDI\) cân tại D

Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)

\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E

c.

Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)

Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)

\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)