\(\left|2x-3\right|=21-x\)

ĐK : \(21-x\ge0\Leftrightarrow x\le21\)

TH1 : \(2x-3=21-x\Leftrightarrow3x=24\Leftrightarrow x=8\)(tm)

TH2 : \(2x-3=-21+x\Leftrightarrow x=-18\)(tm)

Trả lời:

| 2x - 3 | = - x + 21 ( đk: x \(\le\)21 )

=> 2x - 3 = - x + 21 hoặc 2x - 3 = x - 21

<=> 2x + x = 21 + 3 hoặc 2x - x = - 21 + 3

<=> 3x = 24 hoặc x = - 18 

<=> x = 8 ( tm ) hoặc x = - 18 ( tm )

Vậy x = 8; x = - 18 là nghiệm của phương trình.

lx - 4l + 3x = 5

lx - 4l = 5 - 3x

=> x - 4 = +- (5 - 3x)

TH1:

x - 4 = 5 - 3x

x + 3x = 5 + 4

4x = 9

=> x = 9/4

TH2:

x - 4 = -5 + 3x

x - 3x = -5 + 4

-2x = -1

=> x  =1/2

Vay x = 9/4 hoac 1/2

| x - 4 | + 3x = 5

| x - 4 | + 3x = 5 \(\Leftrightarrow\)x - 4 + 3x = 5 khi x \(\ge\)4

\(\Leftrightarrow\)4x = 9

\(\Leftrightarrow\)x = \(\frac{9}{4}\)

( không thỏa mãn điều kiện x \(\ge\)4 )

| x - 4 | + 3x = 5  \(\Leftrightarrow\)x - 4 + 3x = - 5 khi x < 4

\(\Leftrightarrow\)2x = 1

\(\Leftrightarrow\)x = \(\frac{1}{2}\)

Với \(x\ne0;\pm1\)

\(E>0\Rightarrow\frac{x^2}{x-1}>0\Rightarrow x-1>0\)vì \(x^2\ge0\)

\(\Leftrightarrow x>1\)

\(E< 1\Rightarrow\frac{x^2}{x-1}< 1\Leftrightarrow\frac{x^2}{x-1}-1< 0\)

\(\Leftrightarrow\frac{x^2-x+1}{x-1}< 0\Rightarrow x-1< 0\)vì

 \(x^2-x+1=x^2-2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)

\(\Leftrightarrow x< 1\)Kết hợp với đk vậy \(x< 1;x\ne0;-1\)

Trả lời:

\(E=\frac{x^2}{x-1}\left(ĐKXĐ:x\ne0;x\ne\pm1\right)\)

Để E > 0 thì \(\frac{x^2}{x-1}>0\)

\(\Leftrightarrow x-1>0\)( vì x² > 0 )

\(\Leftrightarrow x>1\)

Vậy để E > 0 thì x > 1 

Để E < 1 thì \(\frac{x^2}{x-1}< 1\)

\(\Leftrightarrow\frac{x^2}{x-1}-1< 0\)

\(\Leftrightarrow\frac{x^2-x+1}{x-1}< 0\)

\(\Leftrightarrow\frac{x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}}{x-1}< 0\)

\(\Leftrightarrow\frac{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}{x-1}< 0\)

\(\Leftrightarrow x-1< 0\)( vì \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\))

\(\Leftrightarrow x< 1\)

Vậy để E < 1 thì \(x< 1;x\ne0;x\ne\pm1\)

ĐKXĐ : \(x\ne1\)

Vì E = 0

=> \(\frac{x^2}{x-1}=0\)

=> x² = 0 

<=> x = 0 

Vậy x = 0 thì E = 0

Để \(E=0\) thì \(\frac{x^2}{x-1}=0\left(x\ne1\right)\)

\(=>x^2=0\)

\(=>x=0\)

Vậy để\(E=0\)thì\(x=0\)

A B C F D E

Lấy F đối xứng với A qua D.

\(\widehat{BEA}=\widehat{ACB}+\frac{\widehat{ABC}}{2}=54^0;\) \(\widehat{FAE}=\frac{\widehat{BAC}}{2}=54^0\)\(\Rightarrow\widehat{BEA}=\widehat{FAE}\)

Xét tứ giác BAEF: AE || BF vì ABFC là hình thoi; \(\widehat{BEA}=\widehat{FAE}\)

Suy ra BAEF là hình thang cân. Do đó \(BE=AF=2AD\)hay \(AD=\frac{BE}{2}.\)

\(P=-5x^2-2xy-2y^2+14x+10y-1\)

\(=-\left(4x^2-8x+4\right)-\left(y^2-4y+4\right)-\left(x^2+y^2+2xy-6x-6y+9\right)+16\)

\(=-4\left(x-1\right)^2-\left(y-2\right)^2-\left(x+y-3\right)^2+16\le16\)

Dấu \(=\)khi \(\hept{\begin{cases}x-1=0\\y-2=0\\x+y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\).

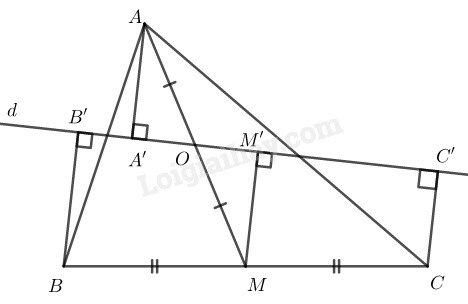
Ta có: \(BB'\perp d\left(gt\right)\)

           \(CC'\perp d\left(gt\right)\)

\(\Rightarrow BB'//CC'\)

\(\Rightarrow BB'CC'\)là hình thang.

Kẻ \(MM'\perp d\)

\(\Rightarrow MM'//BB'//CC'\)

Lại có : \(MM'\)là đường trung bình của hình thang \(BB'CC'\)

\(\Rightarrow MM'=\frac{BB'+CC'}{2}\)\(\left(1\right)\)

Xét tam giác vuông \(AA'O\)và tam giác vuông \(MM'O\)

\(\widehat{OA'A}=\widehat{OM'M}\)

\(AO=MO\left(gt\right)\)

\(\widehat{AOA'}=\widehat{MOM'}\)( đối đỉnh )

=> \(\Delta AA'O=\Delta MM'O\)( cạnh huyền - góc nhọn )

\(\Rightarrow AA'=MM'\left(2\right)\)

Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow AA'=\frac{BB'+CC'}{2}\)

                                                                                                                                               # Aeri # 

Bạn có nhìn thấy hình ko ?

Mk lấy tại nguồn : https://hoidap247.com/cau-hoi/8214

Có gì bạn vào link trên để tham khảo bài nhé

Trả lời:

Mk gửi link bn nhé:

Phần câu trả lời giống vậy đó : 

https://lazi.vn/edu/exercise/cho-hinh-thang-abcd-ab-cd-cac-duong-phan-giac-cua-cac-goc-ngoai-tai-dinh-a-va-d-cat-nhau-tai-m

\(x^{n-2}\left(x^2-1\right)-x\left(x^{n-1}-x^{n-3}\right)\)

\(=x^{n-2+2}-x^{n-2}-x^{1+n-1}+x^{1+n-3}\)

\(=x^n-x^{n-2}-x^n+x^{n-2}=0\)