a: Ta có: \(AE=EB=\dfrac{AB}{2}\)

\(DF=FC=\dfrac{DC}{2}\)

\(AD=BC=\dfrac{AB}{2}\)

mà AB=DC

nên AE=EB=DF=FC=AD=BC

Xét tứ giác AEFD có

AE//FD

AE=FD

Do đó: AEFD là hình bình hành

Hình bình hành AEFD có AE=AD

nên AEFD là hình thoi

Xét tứ giác AECF có

AE//CF

AE=CF

Do đó: AECF là hình bình hành

b: Vì AECF là hình bình hành

nên AF//CE

=>FM//EN

Xét tứ giác BEDF có

BE//DF

BE=DF

Do đó: BEDF là hình bình hành

=>BF//DE
=>FN//EM

Ta có: AEFD là hình thoi

=>AF\(\perp\)DE tại M

Xét tứ giác EMFN có

EM//FN

EN//MF

Do đó: EMFN là hình bình hành

Hình bình hành EMFN có \(\widehat{EMF}=90^0\)

nên EMFN là hình chữ nhật

a: \(2\sqrt{27}-3\sqrt{54}-\dfrac{1}{3}\sqrt{48}\)

\(=2\cdot3\sqrt{3}-3\cdot3\sqrt{6}-\dfrac{1}{3}\cdot4\sqrt{3}\)

\(=6\sqrt{3}-9\sqrt{6}-\dfrac{4}{3}\sqrt{3}=\dfrac{14}{3}\sqrt[]{3}-9\sqrt{6}\)

b: \(-\dfrac{1}{2}\sqrt{108}+\dfrac{1}{15}\cdot\sqrt{75}-\dfrac{1}{3}\cdot\sqrt{363}\)

\(=-\dfrac{1}{2}\cdot6\sqrt{3}+\dfrac{1}{15}\cdot5\sqrt{3}-\dfrac{1}{3}\cdot11\sqrt{3}\)

\(=-3\sqrt{3}+\dfrac{1}{3}\sqrt{3}-\dfrac{11}{3}\sqrt{3}=-\dfrac{19}{3}\sqrt{3}\)

c: \(\dfrac{5}{8}\sqrt{48}-\dfrac{1}{33}\cdot\sqrt{363}+\dfrac{3}{14}\cdot\sqrt{147}\)

\(=\dfrac{5}{8}\cdot4\sqrt{3}-\dfrac{1}{33}\cdot11\sqrt{3}+\dfrac{3}{14}\cdot7\sqrt{3}\)

\(=\dfrac{5}{2}\sqrt{3}-\dfrac{1}{3}\sqrt{3}+\dfrac{3}{2}\sqrt{3}=\dfrac{11}{3}\sqrt{3}\)

d:

ĐKXĐ: x>=0; x<>9

 Sửa đề:\(\dfrac{x-9}{x-3\sqrt{x}}-\dfrac{x-4}{\sqrt{x}+2}\)

\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}\)

\(=\dfrac{\sqrt{x}+3}{\sqrt{x}}-\left(\sqrt{x}-2\right)=\dfrac{\sqrt{x}+3-x+2\sqrt{x}}{\sqrt{x}}\)

\(=\dfrac{-x+3\sqrt{x}+3}{\sqrt{x}}\)

e: ĐKXĐ: x>=0; x<>4

\(\dfrac{x+2\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-2}\)

\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-2}\)

\(=\sqrt{x}+1-\sqrt{x}+2=3\)

a: Vì hệ số góc là -4 nên a=-4

=>y=-4x+b

Thay x=2 và y=-5 vào y=-4x+b, ta được:

b-8=-5

=>b=3

Vậy: y=-4x+3

b: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=2x-1

nên \(\left\{{}\begin{matrix}a=2\\b\ne-1\end{matrix}\right.\)

Vậy: y=2x+b(b\(\ne\)-1)

c: Thay x=0 và y=4 vào y=ax+b, ta được:

\(a\cdot0+b=4\)

=>b=4

=>y=ax+4

Thay x=4/5 và y=0 vào y=ax+4, ta được:

\(\dfrac{4}{5}a+4=0\)

=>\(\dfrac{4}{5}a=-4\)

=>a=-5

vậy: y=-5x+4

d: Vì đồ thị hàm số y=ax+b vuông góc với đường thẳng y=-2x+3 nên -2a=-1

=>\(a=\dfrac{1}{2}\)

Vậy: \(y=\dfrac{1}{2}x+b\)

Thay x=1/4 và y=-5 vào y=1/2x+b, ta được:

\(b+\dfrac{1}{2}\cdot\dfrac{1}{4}=-5\)

=>\(b=-5-\dfrac{1}{8}=-\dfrac{41}{8}\)

a: ĐKXĐ: x+7>=0

=>x>=-7

b: ĐKXĐ: 5x+25>=0

=>5x>=-25

=>x>=-5

c: ĐKXĐ: 15-5x>=0

=>5x<=15

=>x<=3

d: ĐKXĐ: 1-4x>=0

=>4x<=1

=>\(x< =\dfrac{1}{4}\)

a) \(\sqrt{x+7}xđ\Leftrightarrow x+7\ge0\Leftrightarrow x\ge-7\)

b) \(\sqrt{5x+25}xđ\Leftrightarrow5x+25\ge0\Leftrightarrow x\ge-5\)

c) \(\sqrt{15-5x}xđ\Leftrightarrow15-5x\ge0\Leftrightarrow x\le3\)

d) \(\sqrt{1-4x}xđ\Leftrightarrow1-4x\ge0\Leftrightarrow x\le\dfrac{1}{4}\)

Đổi 40 phút =2/3 giờ

Gọi thời gian từ lúc ô tô xuất phát đến khi gặp xe máy là x (giờ)

Quãng đường ô tô đi đến khi gặp xe máy là: \(60x\) (km)

Do xe máy xuất phát trước ô tô 40 phút nên thời gian xe máy đi là: \(x+\dfrac{2}{3}\) giờ

Quãng đường xe máy đi đến khi gặp ô tô là: \(50\left(x+\dfrac{2}{3}\right)\) km

Do 2 xe gặp nhau chính giữa AB nên quãng đường 2 xe đi bằng nhau, ta có pt:

\(60x=50\left(x+\dfrac{2}{3}\right)\)

\(\Rightarrow x=\dfrac{10}{3}\) (giờ)

Độ dài quãng đường AB là: \(60.\dfrac{10}{3}.2=400\) (km)

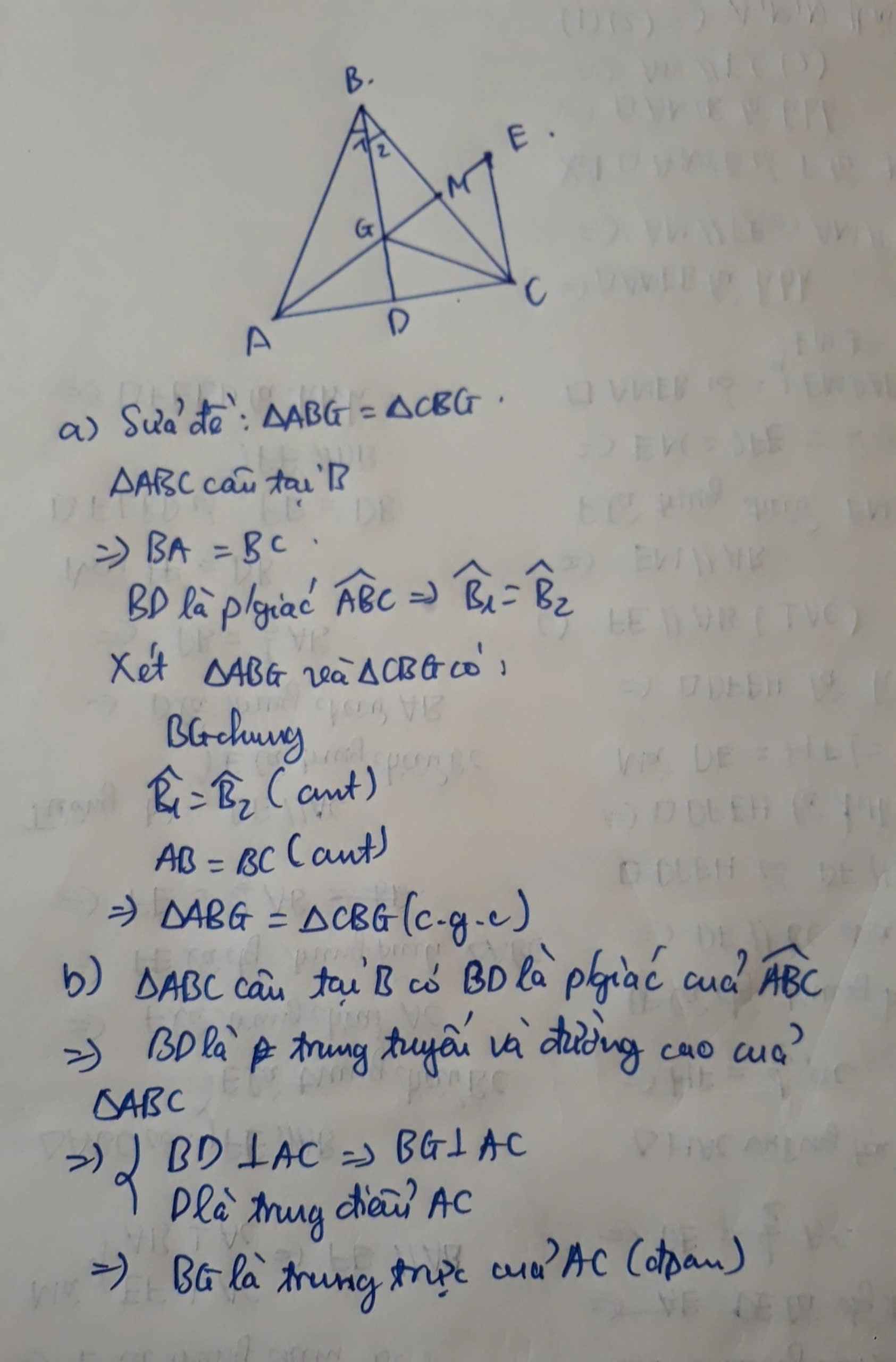
a: Xét ΔBAG và ΔBCG có

BA=BC

\(\widehat{ABG}=\widehat{CBG}\)

BG chung

Do đó: ΔBAG=ΔBCG

=>GA=GC

=>ΔGAC cân tại G 

b: Ta có: BA=BC

=>B nằm trên đường trung trực của AC(1)

Ta có: GA=GC

=>G nằm trên đường trung trực của AC(2)

Từ (1),(2) suy ra BG là đường trung trực của AC

a: \(Q=\left(x-y\right)^2-\left(x-y\right)\left(x+y\right)+\left(x-2y\right)^2\)

\(=\left(x-y\right)\left(x-y-x-y\right)+\left(x-2y\right)^2\)

\(=-2y\left(x-y\right)+x^2-4xy+4y^2\)

\(=-2xy+2y^2+x^2-4xy+4y^2\)

\(=x^2-6xy+6y^2\)

b: \(\left(3x-1\right)^2-\left(x+7\right)^2-\left(2x-5\right)\left(2x+5\right)\)

\(=9x^2-6x+1-x^2-14x-49-\left(4x^2-25\right)\)

\(=8x^2-20x-48-4x^2+25=4x^2-20x-23\)

Yêu cầu của đề bài là gì vậy em?

\(a,y^2+2y+1=y^2+2.y.1+1^2=\left(y+1\right)^2\)

\(b,9x^2+y^2-6xy=\left(3x\right)^2-2\cdot3x\cdot y+y^2=\left(3x-y\right)^2\)

\(c,25a^2+4b^2+20ab=\left(5a\right)^2+2\cdot5a\cdot2b+\left(2b\right)^2=\left(5a+2b\right)^2\)

\(d,x^2-x+\dfrac{1}{4}=x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x-\dfrac{1}{2}\right)^2\)

`y^2 + 2y + 1 = y^2 + 2y .1 + 1^2 + (y+1)^2`

`9x^2 + y^2 - 6xy = (3x)^2 - 2.3x.y + y^2 = (3x + y)^2`

`25a^2 + 4b^2 + 20ab = (5a)^2 + 2.5a .2b + (2b)^2 = (5a + 2b)^2`

`x^2 - x + 1/4 = x^2  - 2x .1/2 +(1/2)^2 = (x-1/2)^2`

Trên tia đối của AB lấy E sao cho AE=DC

Ta có DC//AB => DC//AE

=> AEDC là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hbh)

Do ABCD là hình thang cân

\(\Rightarrow\widehat{BCD}=\widehat{ADC}\) (1)

Ta có AB//CD \(\Rightarrow\widehat{ADC}+\widehat{DAB}=180^o\) (2 góc trong cùng phí bù nhau) (2)

Mà \(\widehat{EAD}+\widehat{DAB}=\widehat{EAB}=180^o\) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{EAD}=\widehat{BCD}\)

Xét tg EAD và tg BCD có

AE = CD; \(\widehat{EAD}=\widehat{BCD}\left(cmt\right)\); AD = BC (gt)

=> tg EAD = tg BCD (c.g.c) => ED=BD => tg BDE cân tại D

Dựng \(DH\perp AB\left(H\in AB\right)\Rightarrow BH=EH=\dfrac{BE}{2}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)

Ta có

AE=CD \(\Rightarrow AB+CD=AB+AE=BE\)

\(DH=\dfrac{1}{2}\left(AB+CD\right)=\dfrac{1}{2}\left(AB+AE\right)=\dfrac{BE}{2}\)

\(\Rightarrow DH=BH=EH=\dfrac{BE}{2}\)

=> tg DHE và tg BHD là tg vuông cân tại H

\(\Rightarrow\widehat{DEH}=\widehat{EDH}=\widehat{BDH}=\widehat{DBH}=45^o\)

\(\Rightarrow\widehat{EDH}+\widehat{BDH}=\widehat{BDE}=45^o+45^o=90^o\Rightarrow ED\perp BD\)

Ta có

ED//AC (cạnh đối hbh AEDC)

\(\Rightarrow AC\perp BD\)