Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
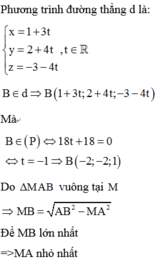
Gọi H là hình chiếu vuông góc của A lên mặt phẳng (P)
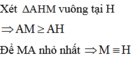
⇒ M B là giao tuyến của mặt phẳng (P) với mặt phẳng α ( α là mặt phẳng chứa d và vuông góc với mặt phẳng (P))
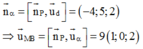
Vậy phương trình đường thẳng MB:
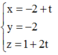
Thấy ngay điểm I(-1;-2;3) thỏa mãn.

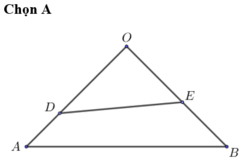
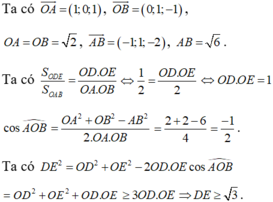
Dấu bằng xảy ra khi và chỉ khi OD = OE = 1
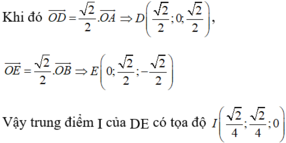
Chú ý: Sau khi chứng minh được OD=OE=1 thì ta có thể tìm trung điểm I của DE như sau:
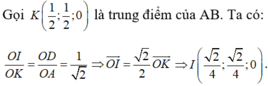

Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm

Chọn C
Ta có AC'=6 nên AB = 2 3 .
Mặt cầu (S) có tâm I(2;4;-1) trùng với tâm hình lập phương ABCD.A'B'C'D' và có bán kính R =1 < A B 2 nên mặt cầu (S) nằm trong hình lập phương ABCD.A'B'C'D'.
Với mọi điểm M nằm trong hình lập phương ABCD.A'B'C'D', tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 3AB = 6 3 .
Vậy từ một điểm M bất kỳ thuộc mặt cầu (S), tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 6 3 .
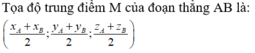

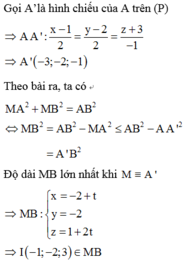

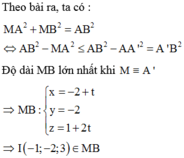
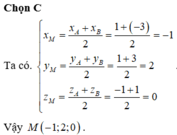

Bài toán thuộc dạng tổ hợp hình học với điều kiện về tọa độ nguyên, khá kinh điển và thú vị. Ta sẽ đi chứng minh rằng:
🚩 Phân tích & định hướng:
\(\left(\right. \frac{x_{1} + x_{2}}{2} , \frac{y_{1} + y_{2}}{2} , \frac{z_{1} + z_{2}}{2} \left.\right)\)
→ Trung điểm có tọa độ nguyên nếu tổng của từng cặp tọa độ đều là số chẵn.
✅ Cách làm: Xét theo parity (chẵn/lẻ)
Bước 1: Có bao nhiêu "kiểu chẵn/lẻ" cho một điểm?
Vì mỗi tọa độ có thể chẵn (0) hoặc lẻ (1) nên mỗi điểm có 3 tọa độ → có:
\(2 \times 2 \times 2 = 8 \&\text{nbsp};\text{ki}ể\text{u}\&\text{nbsp};\text{ch} \overset{\sim}{\overset{ }{\text{a}}} \text{n}/\text{l}ẻ\&\text{nbsp};\text{kh} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{nhau}\)
(Mỗi kiểu được biểu diễn bởi bộ ba bit: \(\left(\right. x \textrm{ } \textrm{ } 2 , y \textrm{ } \textrm{ } 2 , z \textrm{ } \textrm{ } 2 \left.\right)\))
Bước 2: Có 9 điểm → dùng Nguyên lý Dirichlet (Pigeonhole Principle)
→ Chắc chắn tồn tại ít nhất một cặp điểm có cùng kiểu chẵn/lẻ.
Bước 3: Với hai điểm cùng kiểu chẵn/lẻ → Trung điểm có tọa độ nguyên
Ví dụ:
→ Trung điểm có tọa độ nguyên.
✅ Kết luận:
Với 9 điểm bất kỳ có tọa độ nguyên trong không gian \(O x y z\), luôn tồn tại ít nhất một cặp điểm có cùng kiểu chẵn/lẻ tại từng tọa độ → trung điểm của chúng có tọa độ nguyên.