Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')

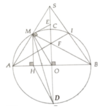
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm
(O;R) là đường tròn tâm
𝑂
O, bán kính
𝑅
R.
𝐶
𝐷
CD là đường kính của
(
𝑂
)
(O),
𝐶
𝐷
=
2
𝑅
CD=2R.
𝑀
M là điểm thay đổi trên đoạn
𝑂
𝐶
OC.
(
𝑂
′
)
(O
′
) là đường tròn đường kính
𝑀
𝐷
MD.
𝐼
I là trung điểm của đoạn
𝑀
𝐶
MC.
Đường thẳng qua
𝐼
I vuông góc với
𝐶
𝐷
CD cắt
(
𝑂
)
(O) tại hai điểm
𝐸
E và
𝐹
F.
Đường thẳng
𝐸
𝐷
ED cắt
(
𝑂
′
)
(O
′
) tại điểm
𝑃
P.
a) Chứng minh ba điểm
𝑃
,
𝑀
,
𝐹
P,M,F thẳng hàng.
Phân tích và hướng dẫn:
Vì
𝐶
𝐷
CD là đường kính
(
𝑂
)
(O), nên
𝑂
O là trung điểm
𝐶
𝐷
CD.
𝑀
M nằm trên
𝑂
𝐶
OC, do đó
𝑀
M nằm trên đoạn
𝑂
𝐶
⊂
𝐶
𝐷
OC⊂CD.
𝐼
I là trung điểm
𝑀
𝐶
MC.
Đường thẳng qua
𝐼
I vuông góc với
𝐶
𝐷
CD cắt đường tròn
(
𝑂
)
(O) tại
𝐸
,
𝐹
E,F.
Ta cần chứng minh
𝑃
,
𝑀
,
𝐹
P,M,F thẳng hàng, trong đó
𝑃
P là giao điểm thứ hai của đường thẳng
𝐸
𝐷
ED với
(
𝑂
′
)
(O
′
).
Phương pháp:
Sử dụng các tính chất về góc nội tiếp, định lý Menelaus hoặc Ceva, hoặc các phép biến đổi hình học.
Sử dụng các phép dựng hình và các quan hệ vuông góc, trung điểm để thiết lập tỷ lệ đoạn thẳng.
Bạn muốn mình giúp chứng minh chi tiết từng bước không?
b) Chứng minh
𝐼
𝑃
IP là tiếp tuyến của đường tròn
(
𝑂
;
𝑅
)
(O;R).
Phương pháp:
Chứng minh
𝐼
𝑃
IP vuông góc với bán kính tại điểm tiếp xúc.
Hoặc dùng hệ thức về tiếp tuyến và dây cung, chứng minh khoảng cách từ tâm đến đường thẳng
𝐼
𝑃
IP bằng bán kính.
c) Tìm vị trí của
𝑀
M trên đoạn
𝑂
𝐶
OC sao cho diện tích tam giác
𝐼
𝑃
𝑂
IPO lớn nhất.
Phương pháp:
Biểu diễn tọa độ các điểm
𝐼
,
𝑃
,
𝑂
I,P,O theo tham số vị trí của
𝑀
M trên
𝑂
𝐶
OC.
Viết biểu thức diện tích tam giác
𝐼
𝑃
𝑂
IPO theo tham số đó.
Tìm giá trị cực đại bằng cách lấy đạo hàm, tìm điểm cực trị.