Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

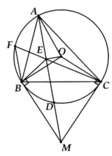
a, O B M ^ = O E M ^ = 90 0
=> Tứ giác OEBM nội tiếp
b, Chứng minh được: ∆ABM:∆BDM (g.g) => M B 2 = M A . M B
c, DOBC cân tại O có OM vừa là trung trực vừa là phân giác
=> M O C ^ = 1 2 B O C ^ = 1 2 s đ B C ⏜
Mà B F C ^ = 1 2 B C ⏜ => M O C ^ = B F C ^
d, O E M ^ = O C M ^ = 90 0 => Tứ giác EOCM nội tiếp
=> M E C ^ = M O C ^ = B F C ^ mà 2 góc ở vị trí đồng vị => FB//AM

a: góc OAD+góc OMD=180 độ
=>OADM nội tiếp
b: ΔOBC cân tại O
mà ON là đường cao
nên ONlà trung trực của BC
=>sđ cung NB=sd cung NC
=>góc BAN=góc CAN
=>AN là phân giác của góc BAC
góc DAI=1/2*sđ cung AN
góc DIA=1/2(sđ cung AB+sđ cung NC)
=1/2(sđ cung AB+sđ cung NB)
=1/2*sđ cung AN
=>góc DAI=góc DIA
=>ΔDAI cân tại D

Do BM là tiếp tuyến của đường tròn nên \widehat{OBM}=90^o
o
Xét đường tròn (O) có AD là một dây cung. Lại có E là trung điểm AD nên theo tính chất của đường kính và dây cung, ta có OE\perp ADOE⊥AD hay \widehat{OEM}=90^oOEM=90o.
Xét tứ giác OEBM có \widehat{OBM}=\widehat{OEM}=90^oOBM=OEM=90o, chúng lại là hai góc kề nhau nên OEBM là tứ giác nội tiếp.
Cho tam giác ABCABC có ba góc nhọn nội tiếp đường tròn tâm OO (AB < AC)(AB<AC). Hai tiếp tuyến tại BB và CC cắt nhau tại MM. AMAM cắt đường tròn (O)(O) tại điểm thứ hai DD. Gọi EE là trung điểm đoạn ADAD. Chứng minh OEBMOEBM là tứ giác nội tiếp.

theo bai ta co E là trung điểm đoạn ADAD
ma AD la mot day cung thuoc (O)
=> OE vuong goc voi AD
hay goc OEM = 90 (1)
Mat khac, BM vuong goc voi OB tai B (gt)
hay goc OBM= 90 (2)
Tu (1) va (2) suy ra tu giac OEBM noi tiep
1. Chứng minh ED vuông góc với BC
Để chứng minh DE vuông góc với BC, ta dựa vào định lý về tia phân giác của góc. Giả sử tam giác ABC vuông tại A và BD là tia phân giác của góc ABC. Theo giả thuyết, ta có E thuộc cạnh BC và DE perpendicular với BC (tại E). Do đó, có thể viết rằng: \(\angle A D E + \angle E D C = 9 0^{\circ}\), điều này chứng tỏ rằng DE vuông góc với BC.2. Chứng minh A, D, F thẳng hàng
Để chứng minh A, D, F thẳng hàng, ta cần chỉ ra rằng các góc liên quan đến ba điểm này tạo thành một góc bẹt (180°). Sử dụng định lý về các góc kề bù, ta có thể thấy rằng:- Nếu \(\angle A D F + \angle D F E = 18 0^{\circ}\) hoặc \(\angle A D F + \angle A D E = 18 0^{\circ}\), thì ta kết luận rằng A, D, F thẳng hàng.
Cụ thể hơn, ta có thể chứng minh thông qua việc sử dụng tính chất tam giác vuông và các bội số cạnh của tam giác ABC; khi đó, tất cả góc này sẽ liên kết lại với nhau trở về cùng một đường thẳng, làm cho ba điểm A, D, và F thẳng hàng.Kết luận
Như vậy, từ các chứng minh này, ta có thể kết luận rằng DE vuông góc với BC và ba điểm A, D, F thẳng hàng. Mọi lý thuyết và chứng minh sâu hơn có thể tham khảo trong tài liệu hình học. Chúc bn hok tốt và tick mk nha