K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
29 tháng 5 2017
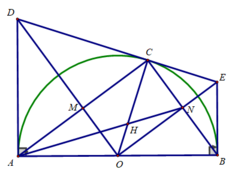
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

12 tháng 1 2023
a: Xét tứ giác ABDC có
AC//BD
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
b: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
c: Xét (O) có
CA,CM là tiêp tuyến
nên CA=CM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB
CM+MD=CD
=>AC+BD=CD
Sửa đề: Đường kính BC
a: Xét (O) có
QM,QC là các tiếp tuyến
Do đó: QM=QC và OQ là phân giác của góc MOC
QM=QC
=>Q nằm trên đường trung trực của MC(1)
Ta có: OM=OC
=>O nằm trên đường trung trực của MC(2)
Từ (1),(2) suy ra OQ là đường trung trực của MC
=>OQ\(\perp\)MC tại H và H là trung điểm của MC
H là trung điểm của MC nên HM=HC
b: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
=>BM\(\perp\)MC
mà MC\(\perp\)OQ
nên OQ//BM
=>BMQO là hình thang
c: Xét (O) có
KB,KM là các tiếp tuyến
Do đó: KB=KM và OK là phân giác của góc MOB
BK+QC=KM+MQ=KQ
d: Ta có: OK là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOK}\)
Ta có: OQ là phân giác của góc MOC
=>\(\widehat{MOC}=2\cdot\widehat{MOQ}\)
Ta có: \(\widehat{MOB}+\widehat{MOC}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{MOK}+\widehat{MOQ}\right)=180^0\)
=>\(2\cdot\widehat{KOQ}=90^0\cdot2\)
=>\(\widehat{KOQ}=90^0\)
e: Xét ΔOKQ vuông tại O có OM là đường cao
nên \(MK\cdot MQ=OM^2\)
=>\(BK\cdot QC=OM^2=R^2\)
Tick cho mình với nhé!!!
a) Do OQ là bán kính vuông góc với tiếp tuyến tại Q, ta có OQ vuông góc với CY. Tam giác OMC là tam giác cân tại O (vì OM = OC, đều là bán kính của nửa đường tròn). Đường thẳng OQ là đường trung trực của đoạn thẳng MC, nên MH = HC (đpcm)
b) Xét các tính chất:
-OQ và OB là bán kính vuông góc với các tiếp tuyến tại Q và B, nên góc BOQ = 90 độ.
-Góc BMQ = BOQ = 90 độ.
Vì tứ giác BMQO có các góc vuông và tiếp xúc với nửa đường tròn, nên BMQO là một tứ giác nội tiếp hình chữ nhật.
c) Trong tam giác vuông OBK, BK là tiếp tuyến từ B, nên BK = OM (theo tính chất tiếp tuyến cắt nhau từ một điểm).
Trong tam giác vuông OQK, KQ = OQ + BK. Do OC = OQ, ta có BK + OC = KQ (đpcm)
d) Do OQ là bán kính vuông góc với tiếp tuyến tại Q và OK là bán kính vuông góc với tiếp tuyến tại K, nên góc KOQ = 90 độ (đpcm)
e)Do BK và CQ là hai tiếp tuyến từ các điểm B và C lần lượt đến M, ta áp dụng tính chất của tiếp tuyến, có tích các khoảng cách tiếp tuyến bằng bình phương bán kính:
BK × CQ = OM² = r² (đpcm)