Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

10³ + 2¹⁵
= 1000 + 32768
= 33768
Mà 33768 : 33 = 1023 (dư 9)
Em xem lại đề


M = 22010-(22009 + 22008+....+21+20
Đặt A =( 22009+22008+...21 +20)
Suy ra 2A = 22010+22009+22008+...22+2
Suy ra 2A-A = ( 22010+22009+22008+...+22+2) - (22009+ 22008+...+21+20)
Suy ra A= 22010-20
Suy ra M = 22010-A=22010 - 22010+20=1
Vậy M=1
Đúng nha

ĐKXĐ : 2x \(\ge\)0 <=> x \(\ge\)0
| 7 + x | = 2x <=> \(\orbr{\begin{cases}7+x=2x\\7+x=-2x\end{cases}}\)
<=> \(\orbr{\begin{cases}x=7\\x=\frac{-7}{3}\end{cases}}\)( KTMĐK)
Vậy x = 7


(x+1)+(x+2)+(x+3)=4x
x+1+x+2+x+3=4x
(x+x+x)+(1+2+3)=4x
x*3+6=4x
6=1*x(bớt cả hai vế đi 3*x)
x=6/1(Tìm thừa số)
x=6

Cho đa thức
P(x)= x mũ 2 + 2x mũ 2 +1 (1)
Thay P(-1) vào đa thức (1) , ta có :
P= \((-1)^2 +2.(-1) ^3\)
P= \(1+ (-2)\)
P= \(-1\)
Thay P(\(\dfrac{1}{2}\)) vào đa thức (1) , ta có :
\(P= (\dfrac{1}{2})^2 +2.(\dfrac{1}{2})^3\)
\(P= \dfrac{1}{4} + \dfrac{1}{4}\)
\(P=\dfrac{1}{2}\)
Q(x)=x mũ 4 +4x mũ 3 +2x mũ 2 trừ 4x+ 1. (2)
Thay Q(-2) vào đa thức (2) , ta có :
Q =\((-2)^4 +4.(-2)^3 +2.(-2)^2-4(-2)+1\)
\(Q = 16-32+8+8+1\)
\(Q= 1\)
Thay Q(1) vào đa thức (2) , ta có:
\(Q= \) \(1^4+4.1^3+2.1^2-4.1+1\)
\(Q= 1+ 4+2-4+1\)
\(Q= 4\)
Tính P(-1) ; P(1/2) ; Q(-2) ; Q(1)

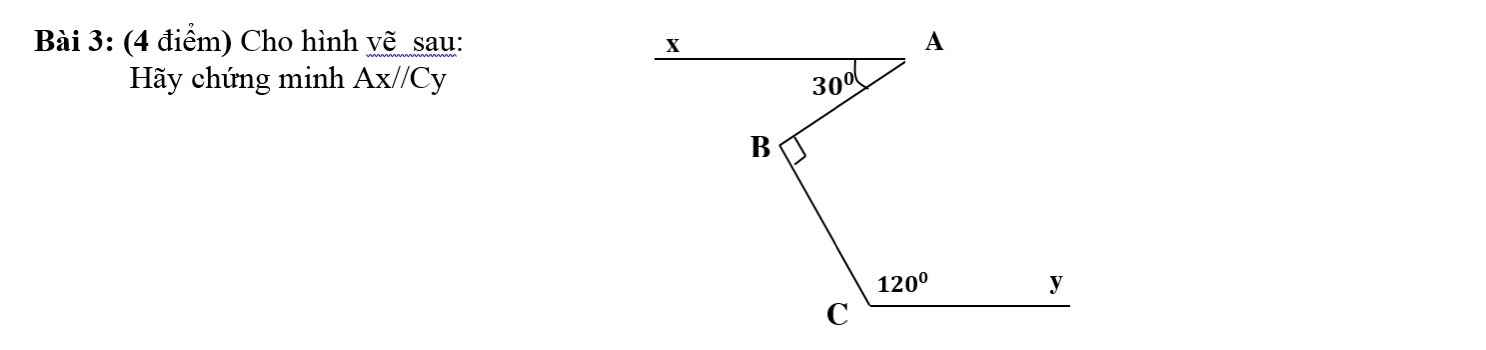
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
x2 - 4x = x2 - 3x
-4x + 3x = x2 - x2
-x = 0
Vậy x = 0