
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


| x - 2,4| = \(\dfrac{1}{2}\)
\(\left[{}\begin{matrix}x-2,4=\dfrac{1}{2}(đk:x>2,4)\\x-2,4=-\dfrac{1}{2}(đk:x< 2,4)\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{1}{2}+2,4\\x=-\dfrac{1}{2}+2,4\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2,9(tm)\\x=1,9(tm)\end{matrix}\right.\)
vậy \(x\in\) { 1,9 ; 2,9}

a, \(\dfrac{3}{7}\)\(x\) - 0,4 = - \(\dfrac{17}{35}\)
\(\dfrac{3}{7}\)\(x\) = - \(\dfrac{17}{35}\) + 0,4
\(\dfrac{3}{7}\)\(x\) = - \(\dfrac{3}{35}\)
\(x\) = - \(\dfrac{3}{35}\): \(\dfrac{3}{7}\)
\(x\) = - \(\dfrac{1}{5}\)
b, 0,2.(\(x\) - 3) +2,4 = 10
0,2.(\(x\) - 3) = 10 - 2,4
0,2.(\(x\) - 3) = 7,6
\(x\) - 3 = 7,6:0,2
\(x\) - 3 = 38
\(x\) = 38 + 3
\(x\) = 41

3/4 - (x - 2/3) = 1 1/3
3/4 - x + 2/3 = 4/3
-x = 4/3 - 3/4 - 2/3
-x = -1/12
x = 1/12
3/4 - (x - 2/3) = 1 1/3
3/4 - x + 2/3 = 4/3
-x = 4/3 - 3/4 - 2/3
-x = -1/12
x = 1/12

a) x + 2/5 = -4/3
x = -4/3 - 2/5
x = -26/15
b) -5/6 + 1/3 x = (-1/2)²
-5/6 + 1/3 x = 1/4
1/3 x = 1/4 + 5/6
1/3 x = 13/12
x = 13/12 : 1/3
x = 13/4
c) 7/12 - (x + 7/6) . 6/5 = (-1/2)³
7/12 - (x + 7/6) . 6/5 = -1/8
(x + 7/6) . 6/5 = 7/12 + 1/8
(x + 7/6) . 6/5 = 17/24
x + 7/6 = 17/24 : 6/5
x + 7/6 = 85/144
x = 85/144 - 7/6
x = -83/144
\(a,x+\dfrac{2}{5}=-\dfrac{4}{3}\\ \Rightarrow x=-\dfrac{26}{15}\\ b,-\dfrac{5}{6}+\dfrac{1}{3}x=\left(-\dfrac{1}{2}\right)^2\\ \Rightarrow-\dfrac{5}{6}+\dfrac{1}{3}x=\dfrac{1}{4}\\ \Rightarrow\dfrac{1}{3}x=\dfrac{13}{12}\\ \Rightarrow x=\dfrac{13}{4}\\ c,\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\left(-\dfrac{1}{2}\right)^3\\ \Rightarrow\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=-\dfrac{1}{8}\\ \Rightarrow\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\dfrac{17}{24}\\ \Rightarrow x+\dfrac{7}{6}=\dfrac{85}{144}\\ \Rightarrow x=-\dfrac{83}{144}.\)

2/3 - |x - 1/2| = 2/3
|x - 1/2| = 2/3 - 2/3
|x - 1/2| = 0
x - 1/2 = 0
x = 0 + 1/2
x = 1/2

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
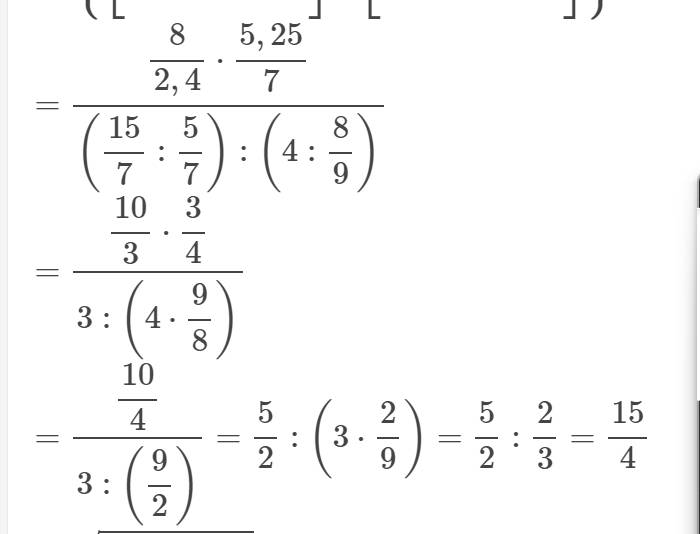

1)
a) \(\frac{x}{6}\)= \(\frac{7}{3}\)
\(\Rightarrow\)x.3=6.7
\(\Rightarrow\)x.3=42
\(\Rightarrow\)x =42:3
\(\Rightarrow\)x =14
b) làm tương tự như câu a
c) làm tương tự như câu
d) làm tương tư như câu a nhưng hơi phúc tạp một chút là bn phải đổi ra từ hỗn số ra phân số hoặc số nguyên
e) tương tự câu d
f) làm tương tự như câu d
2)
a) 3x:\(\frac{27}{10}\)=\(\frac{1}{3}\): \(2\frac{1}{4}\)
3x: \(\frac{27}{10}\) = \(\frac{1}{3}\): \(\frac{9}{4}\)
3x: \(\frac{27}{10}\) = \(\frac{4}{27}\)
3x = \(\frac{4}{27}\). \(\frac{27}{10}\)
3x = \(\frac{2}{5}\)
x = \(\frac{2}{5}\): 3
x = \(\frac{2}{15}\)
Các câu còn lại bn làm tương tự như câu a nha
3)
Làm tương tự như bài 2 nha
mik khuyên bn nếu bn giải bài thì bn nên đổi ra cùng một kiểu số thì tốt hơn như số số thập phân thì thập phân hết ấy
Cuối cùng chúc bn học giỏi

1 a) \(\dfrac{\left(-2\right)}{5}\)= \(\dfrac{-6}{15}\); \(\dfrac{15}{-6}\)= \(\dfrac{5}{-2}\); \(\dfrac{-6}{-2}\)= \(\dfrac{15}{5}\); \(\dfrac{-2}{-6}\)= \(\dfrac{5}{15}\)

a, \(\dfrac{5}{2}\)\(x\) - \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\)
\(\dfrac{5}{2}\)\(x\) = \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)
\(\dfrac{5}{2}\)\(x\) = 1
\(x\) = 1: \(\dfrac{5}{2}\)
\(x\) = \(\dfrac{2}{5}\)
b, \(\dfrac{x+4}{20}\) = \(\dfrac{5}{x+4}\) (đk \(x\) ≠ -4)
(\(x\)+4).(\(x\) + 4) = 20.5
(\(x\)+ 4)2 = 100
(\(x\) + 4)2 = 102
\(\left[{}\begin{matrix}x+4=-10\\x+4=10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-10-4\\x=10-4\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-14\\x=6\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-14; 6}
\(\dfrac{2}{3}-\left|x-2,4\right|=\dfrac{1}{2}\)
\(\left|x-2,4\right|=\dfrac{2}{3}-\dfrac{1}{2}\)
\(\left|x-2,4\right|=\dfrac{1}{6}\)
*) Với \(x\ge2,4\) ta có:
\(x-2,4=\dfrac{1}{6}\)
\(x=\dfrac{1}{6}+2,4\)
\(x=\dfrac{77}{30}\) (nhận)
*) Với \(x< 2,4\) ta có:
\(x-2,4=-\dfrac{1}{6}\)
\(x=-\dfrac{1}{6}+2,4\)
\(x=\dfrac{67}{30}\) (nhận)
Vậy \(x=\dfrac{67}{30};x=\dfrac{77}{30}\)