
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình mong bạn sẽ viết câu hỏi rỏ ràng hơn. "Các cách để trả lời toán hình 6 " !!! KHÓ HIỂU QUÁ. Bn phải hỏi là các cách chứng minh tia nằm giữa, tia phân giác, góc, hay là tam giác j chứ.
Xin lỗi nhưng mk ko giúp bạn đc. Chúc bạn học tốt

C1 : Liệt kê phần tử của tập hợp
C2 : Chỉ ra tính chất đặc trưng của tập hợp
phần tử của một tập hợp chính là số hay gì đó,khó giải tích lắm.
Vd:
- Có thể xác định một tập hợp bằng cách liệt kê các phần tử của chúng giữa cặp dấu { }, chẳng hạn:
C = {4, 2, 1, 3}
D = {Đ;O;T;R;A;N;G;X;H}
Các tập hợp có nhiều phần tử có thể liệt kê một số phần tử. Chẳng hạn tập hợp 1000 số tự nhiên đầu tiên có thể liệt kê như sau:
{0, 1, 2, 3,..., 999},
Tập các số tự nhiên chẵn có thể liệt kê:
{2, 4, 6, 8,... }.
trong này A,B chính là phần tử

Các số nguyên tố từ 2 đến 100
2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 2
Tính chất của số nguyên tố
Kí hiệu là ''b / a'' nghĩa là b là ước của a, kí hiệu a \(⋮\) b nghĩa là a chia hết cho b
1. Ước tự nhiên khác 1 nhỏ nhất của 1 số tự nhiên là nguyên tố
Chứng minh; Giả sử d / a nhỏ nhất; d \(\ne\) 1.
Nếu d không nguyên tố \(\Rightarrow\) d \(=\) d1. d2 ; d1, d2 lớn hơn 1
\(\Rightarrow\) d1 / a với d1 lớn hơn d ; mâu thuẫn với d nhỏ nhất. Vậy d là nguyên tố
2. Cho p là nguyên số; a \(\in\) N; a \(\ne\) 0. Khi đó
a,b \(=\) p \(\Leftrightarrow\) a \(⋮\) p
a,b \(=\) 1\(=\) a p
3. Nếu tích của nhiều số chia hết cho một số nguyên tố p thì có ít nhất một thừa số chia hết cho p
\(II\) ai \(⋮\) p \(\Rightarrow\) \(\exists\)ai \(⋮\)p
4. Ước số dương bé nhất khác 1 của số nguyên tố không vượt qua \(\sqrt{a}\)
5. 2 số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất
6. Tập hợp các số nguyên là vô hạn. Tương đương với viếc ko có nguyên số lớn nhất
Chứng minh; Giả sử có hữu hạn số nguyên tố; p1 bé hơn p2 bé hơn .... pn
Nhật xét a \(=\) p1. p2 .... pn + 1
Ta có; a lớn hơn 1 và a 1 pi; ''i\(=\) a là hợp số, a có nguyên tố pi, hay aMpi và pi M pi. 1M pi ; Mâu thuẫn
Vậy tập hợp các số nguyên tố là vô hạn
Chúc bạn học giỏi

a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}
a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}

Bạn tham khảo : Luyện tập - Bài 66 Sách giáo khoa trang 34 - Toán lớp 6 | Học trực tuyến



Ta có:
A = {15; 26}
B = {1; a; b}
M = {bút}
H = {sách; vở; bút}.
Bạn học lớp 6 à . Năm nay mình học lớp 7 nhưng vẫn nhớ bài Bài 4 trang 6 SGK Toán 6 tập 1 . Kb có gì khó hỏi mk nha
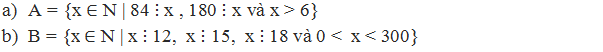
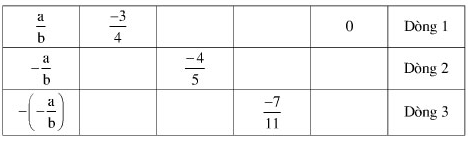
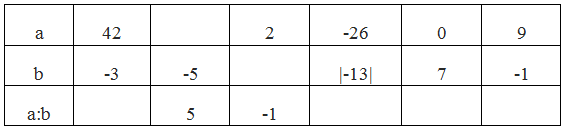
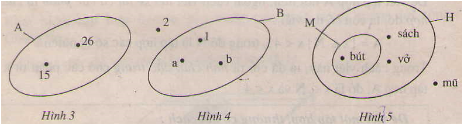
Tập hợp là tập hợp con của A và B chỉ chứa những chữ cái có mặt trong cả A và B.