Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC

Lời giải:
a.
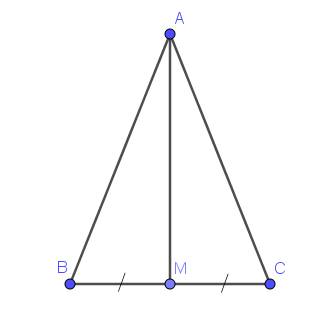
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

A B C M
a/ Câu này không chỉ có 1 cách mình trình bày!
Xét tam giác ABM và tam giác ACM có:
góc BAM = góc CAM (gt)
AM: chung
AB = AC (tam giác ABC cân tại A)
=> tam giác ABM = tam giác ACM (c.g.c)
b/ Vì tam giác ABC cân tại A => AM vừa là đường phân giác vừa là đường cao
PS: Học tính chất tam giác cân là làm được


 Bài 1. Cho tam giác ABC cân tại A có Â = 80o
Bài 1. Cho tam giác ABC cân tại A có Â = 80o
a, Tam giác ABC cân tại A nên \(\widehat{B}\) = \(\widehat{C}\)
⇒ \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)
AB = AC (2)
\(\widehat{BAM}\) = \(\widehat{CAN}\) = 900 (3)
Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)
b, BM = CN ( Δ BAM = ΔCAN)
BM = BN + MN = MN + MC
⇒ BN = CM
c, \(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) =1200
\(\Rightarrow\) \(\widehat{BAN}\) = 1200 - \(\widehat{NAC}\) = 1200 - 900 = 300
\(\widehat{ABN}\) = (1800 - 1200) : 2 = 300
⇒ \(\widehat{BAN}\) = \(\widehat{ABN}\) = 300 ⇒ △ANB cân tại N
a) Xét hai tam giác BADBAD và BFDBFD có:
ABD^=FBD^ABD
=FBD
(vì BDBD là tia phan giác của góc BB);
AB=BFAB=BF (ΔABFΔABF cân tại BB);
BDBD là cạnh chung;
Vậy ΔBAD=ΔBFDΔBAD=ΔBFD (c.g.c).
b) ΔBAD =Δ BFDΔBAD =Δ BFD suy ra BAD^=BFD^=100∘BAD
=BFD
=100∘ (hai góc tương ứng).
Suy ra DFE^=180∘−BFD^=80∘DFE
=180∘−BFD
=80∘. (1)
Tam giác ABCABC cân tại AA nên B^=C^=180∘−100∘2=40∘B
=C
=2180∘−100∘=40