Write your predictions about a future city in Vietnam in an eamil of 160-180 words to a friend.
Outline:
To:
Subject:
Dear___,
I received your email last week, but I couldn't answer your question right away. You asked me what Ha Noi would look like forty years from now. What a difficult question! To tell you the truth, I have had to think very hard and have finally come up with two predictions.
If I take an optimistic viewpoint, ___________________________________.
But if I take the pessimistic viewpoint, _______________________________.
I hope you are satisfied with my answer. And here is my question: What will ______’s capital city look like in the future? I'm looking forward to your reply.
With best wishes,
_____


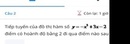
 Giúp em câu 3 với ạ.
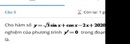
Giúp em câu 3 với ạ.

Dear Anne(Hà Lam).
I received your email last week, in which you asked me about my city New York in 2050. There are different ideas about this question. I thought it in a few days, and now I can give you two predictions.
Let's take a look at an optimis viewpoint. In 2050 New York will become a more liveable city than ever before for lots of reasons. The city authorities have built a very careful plan to promote self-driving electric taxis to deal with crowded public transport. In addition, the city dwellers are encouraged to use city's building roofs for gardens fertilised with compose in order to recycle rubbish and reduce pollution. The government will also build offshore windfarms to replace ageing electricity network.
On the other hand, pessimis people think that the city life won't be a safe place to live in because the government cannot control the use of guns, and therefore the crime rate will be higher. People's life will also continue to be threatened because of natural disasters such as floods, storms, earthquakes. The effects of global warming have great impacts on the city dwellers.
That's all about my answer to your question. I hope you will be satisfied with it, Nam.
Best wishes,
Wonie(Quyên)
tham khảo ạ
Dear Bich
Your last email asked me about my city Ha Noi in 2050. Well, but I'm busy and have no time to reply you soon. Today I am writing to you about that question. There are different ideas about this question. I thought about it in a few days, and now I can give you some predictions.
Let's take a look at optimis aspects. In 2050 Ha Noi will become a more modern city for lots of reasons. High technology has been applied in our lives. The robots will replace us for many jobs such as manufacturing, farming, etc. Smart cars which will be commonly used in the road. They will help human beings to decrease the accidents as well as traffic jams.
On the contrary, pessimis people think that the city life will be a dangerous place to live in because the environment is completely polluted. The effects of global warming have great impacts on the city dwellers, higher temperature in the summer and colder climate in the winter. There are a lot of means of transport so that emission from them cause air pollution. Our health will be threatened because of low air quality index.
That's all about my thoughts about your question. I hope you will be satisfied with it, Bich.
Best wishes,
Chau