CH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 12 2018
\(log_2\left(1+log_{3^{-2}}x-log_{3^2}x\right)< 1\)
\(\Leftrightarrow log_2\left(1-\dfrac{1}{2}log_3x-\dfrac{1}{2}log_3x\right)< 1\)
\(\Leftrightarrow log_2\left(1-log_3x\right)< 1\)
\(\Leftrightarrow0< 1-log_3x< 2\)
\(\Leftrightarrow-1< log_3x< 1\)
\(\Leftrightarrow\dfrac{1}{3}< x< 3\Rightarrow\left\{{}\begin{matrix}a=3\\b=3\end{matrix}\right.\) \(\Rightarrow a=b\)
4 tháng 5 2016
Ta có \(\frac{1}{11};\frac{1}{12};\frac{1}{13};...;\frac{1}{19}>\frac{1}{20}\)
- Suy ra S > \(\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+...+\frac{1}{20}+\frac{1}{20}\)( có 10 số hạng)=\(\frac{10}{20}=\frac{1}{2}\)
- Vậy S>\(\frac{1}{2}\)
4 tháng 5 2016
Ta có S=1/11+1/12+1/13+...+1/20(có 10 phân số)
S>1/20+1/20+1/20+...+1/20(có 10 phân số)
S<10/20=1/2
Nên tổng của S>1/2
Q
31 tháng 3 2017
Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a), b) và với đường thẳng y = -1 ở câu c).
a) Xét hàm số y = x3 – 3x2 + 5 . Tập xác định : R.
y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0,x = 2.
Bảng biến thiên:
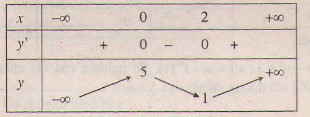
Đồ thị như hình bên.
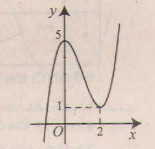
Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
b) Xét hàm số y = -2x3 + 3x2 - 2 . Tập xác định : R.
y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.
Đồ thị như hình bên. Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
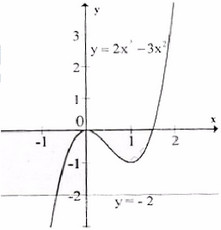
c) Xét hàm số y = f(x) = 2x2 - 2x4. Tập xác định : R.
y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
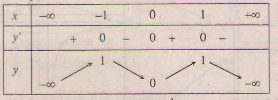
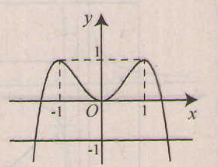
Đồ thị hàm số f(x) và đường thẳng y = -1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.
MW
0
AH
Akai Haruma
Giáo viên
24 tháng 7 2017
Câu 1:
Theo dữ kiện đề bài ta có:
\( \bullet \) PT \(y'=3ax^2+2bx+c=0\) nhận \(x=0\) và \(x=2\) là nghiệm
\(\Rightarrow \left\{\begin{matrix} c=0\\ 3a.2^2+2b.2+c=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} c=0\\ 12a+4b=0(1)\end{matrix}\right.\)
\(\bullet\) \(\left\{\begin{matrix} y(0)=d=0\\ y(2)=a.2^3+b.2^2+c.2+d=-4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} d=0\\ 8a+4b+c+d=-4\leftrightarrow 8a+4b=-4(2)\end{matrix}\right.\)
Từ \((1),(2)\Rightarrow a=1,b=-3\)
Do đó pths thu được là : \(y=x^3-3x^2\)
Câu 2:
Có \(y=-x^3+3mx+1\)
\(\Rightarrow \) \(y'=-3x^2+3m=0\Leftrightarrow x^2=m\). Như vậy, để HS có hai cực trị thì \(m>0\)
Khi đó, hai điểm cực trị đó là \(A(\sqrt{m},2\sqrt{m^3}+1)\) và \(B(-\sqrt{m},1-2\sqrt{m^3})\)
Vì \(OAB\) là tam giác vuông tại $O$ lên \(\overrightarrow{OA}\perp \overrightarrow {OB}\Leftrightarrow (\sqrt{m},2\sqrt{m^3}+1)\perp (-\sqrt{m},1-2\sqrt{m^3})\)
\(\Leftrightarrow -\sqrt{m}\sqrt{m}+(1-2\sqrt{m^3})(1+2\sqrt{m^3})=0\Leftrightarrow -m+1-4m^3=0\Rightarrow m=\frac{1}{2}\)
(thỏa mãn điều kiện)
Vậy \(m=\dfrac{1}{2}\)