DN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 3 2017
\(y=\dfrac{\left(x+1\right)}{\sqrt{1-x}}\)
\(y^2=\dfrac{\left(x+1\right)^2}{1-x}\)
\(y'=\dfrac{2\left(x+1\right)\left(1-x\right)+\left(x+1\right)^2}{2.\left(1-x\right)^2.\dfrac{\left(x+1\right)}{\sqrt{1-x}}}\)
còn non và xanh lắm
28 tháng 3 2017
a : \(y=\dfrac{1}{\left(x^2-x+1\right)^5}=\left(x^2-x+1\right)^{-5}\)
\(\Rightarrow y'=-5\left(2x-1\right)\left(x^2-x+1\right)^{-6}=\dfrac{5-10x}{\left(x^2-x+1\right)^6}\)
b: \(y=x^2+x^{\dfrac{3}{2}}+1\Rightarrow y'=2x+\dfrac{3}{2}x^{\dfrac{1}{2}}=2x+\dfrac{3\sqrt{x}}{2}\)
\(y=\sqrt{\dfrac{x^2+1}{x}}=\left(\dfrac{x^2+1}{x}\right)^{\dfrac{1}{2}}\Rightarrow y'=\dfrac{1}{2}\left(\dfrac{x^2+1}{x}\right)'\left(\dfrac{x^2+1}{x}\right)^{\dfrac{-1}{2}}=\dfrac{x^2-1}{2x^2}\times\dfrac{1}{\sqrt{\dfrac{x^2+1}{x}}}=\dfrac{x^2-1}{2x^2\sqrt{\dfrac{x^2+1}{x}}}\)
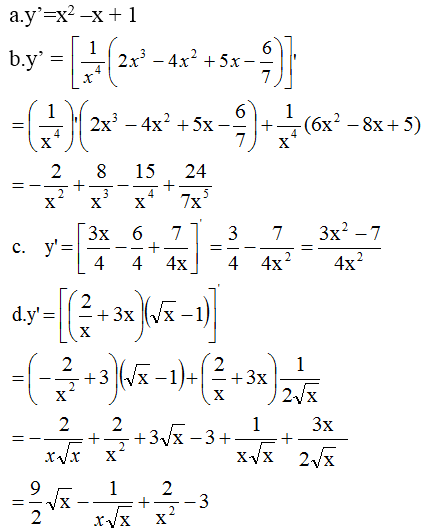
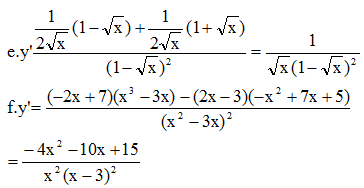
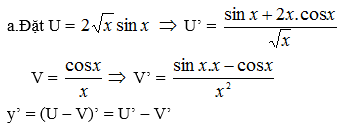
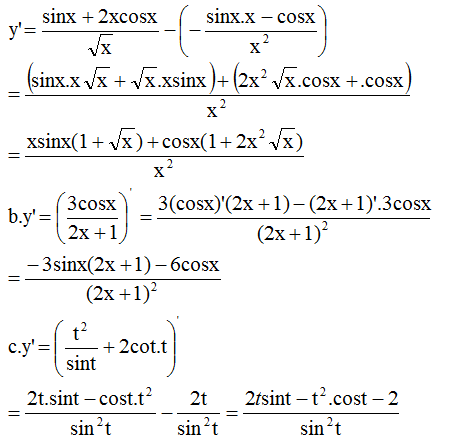
Đề bài yêu cầu điều gì nhỉ?