y/(2 - y) + (y ^ 2 + 2y)/(2y + 2) * ((y + 2)/(y ^ 2 - 2y) - y/(y ^ 2

Khách

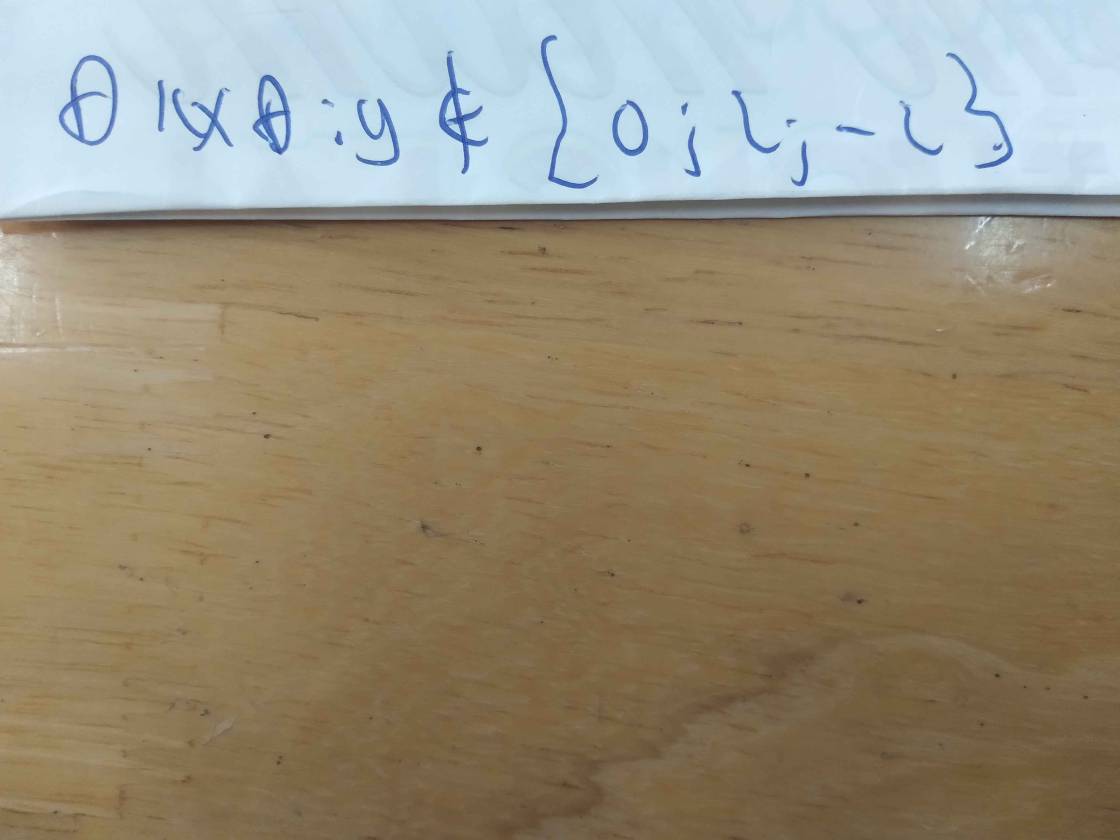
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Trương Trung Hiếu

27 tháng 2 - olm

y/(2 - y) + (y ^ 2 + 2y)/(2y + 2) * ((y + 2)/(y ^ 2 - 2y) - y/(y ^ 2 - 4))

#Toán lớp 8

Nguyễn Lê Phước Thịnh

27 tháng 2

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Thơ Nụ =))

18 tháng 1

cho 2 số thực `x,y` thỏa mãn `x>0,y>2,x`$\ne$`2y`. CMR: $\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}\right)\left(2x^2+y+2\right):\dfrac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}=\dfrac{x+1}{2y-x}$

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

19 tháng 1

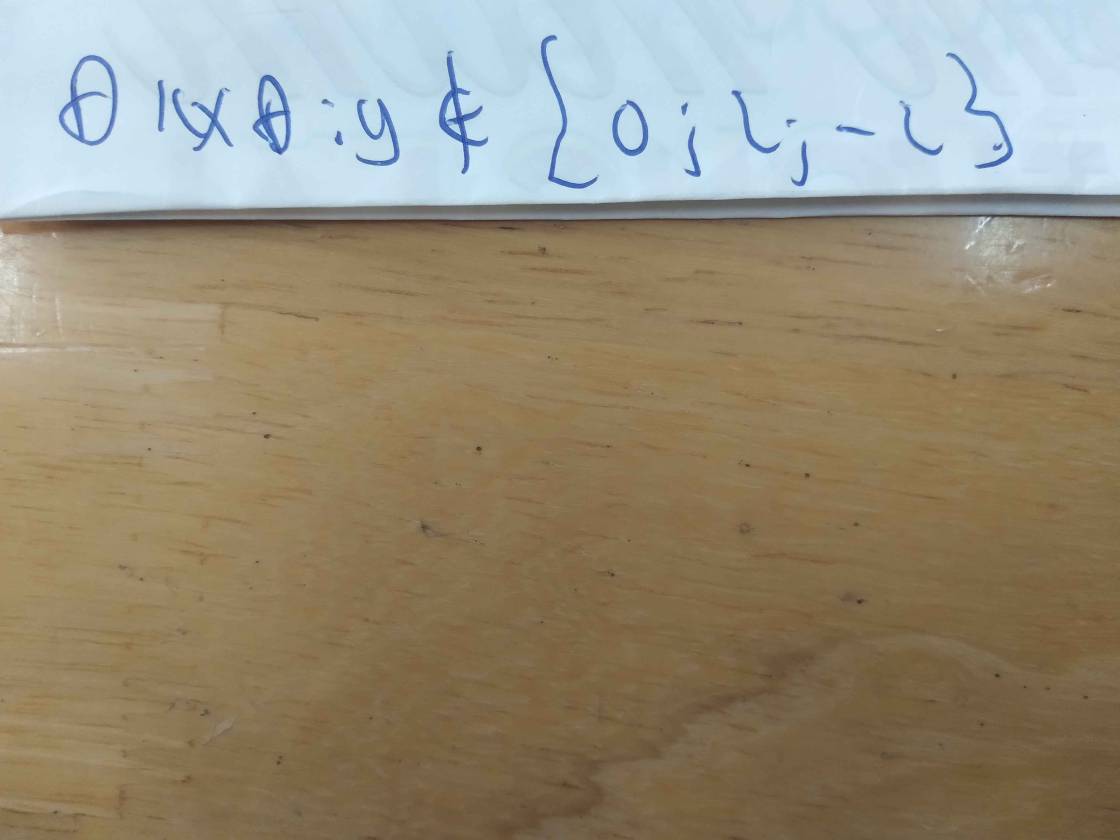
Đề bài sai, đề đúng thì phân thức đằng sau dấu chia phải là:

$\dfrac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}$

Đúng(0)

Duong Thi Nhuong

4 tháng 7 2016

Rút gọn: $\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+xy+x+y}:\frac{x+1}{2y^2+y+2}$

#Toán lớp 8

MInemy Nguyễn

26 tháng 3 2020

chứng minh đẳng thức

$\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}:\frac{1}{2x^2+y+2}=\frac{x+1}{2y-x}$

#Toán lớp 8

Duong Thi Nhuong

30 tháng 9 2016

Rút gọn : $\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+xy+x+y}:\frac{x+y}{2x^2+y+2}$

#Toán lớp 8

Nguyễn Lê Phước Thịnh

12 tháng 2 2022

$=\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-2xy+xy-2y^2}\right):\dfrac{\left(2x^2+y\right)^2-4}{x\left(x+y\right)+\left(x+y\right)}:\dfrac{x+y}{2x^2+y+2}$

$=\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{\left(x-2y\right)\left(x+y\right)}\right)\cdot\dfrac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}\cdot\dfrac{2x^2+y+2}{x+y}$

$=\dfrac{y^2-x^2-x^2-y^2-y+2}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{x+1}{2x^2+y-2}$

$=\dfrac{-\left(2x^2+y-2\right)}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{x+1}{2x^2+y-2}=\dfrac{-\left(x+1\right)}{\left(x-2y\right)\left(x+y\right)}$

Đúng(0)

Nỗi Buồn Không Tên

14 tháng 9 2021

Tìm y
a) 2y(y-1)-y(-4+2y)+4=0
b) (2y+3)(y+2)-(y-4)(2y-1)=18

#Toán lớp 8

Minh Hiếu

14 tháng 9 2021

b)$\left(2y+3\right)\left(y+2\right)-\left(y-4\right)\left(2y-1\right)=18$

⇒$2y^2+4y+3y+6-2y^2+y+8y+4=18$

⇒16y+10=18

⇒16y=28

⇒y=$\dfrac{7}{4}$

Đúng(2)

Minh Hiếu

14 tháng 9 2021

a)$2y\left(y-1\right)-y\left(-4+2y\right)+4=0$

⇒$2y^2-2y+4y-2y+4=0$

⇒2y+4=0

⇒2y=-4

⇒y=-2

Đúng(1)

Duong Thi Nhuong

5 tháng 4 2017

Rút gọn $\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\dfrac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}:\dfrac{1}{2x^2+y+2}$

#Toán lớp 8

Đạt Phạm

4 tháng 7 2017 - olm

rút gọn biểu thức :

a) (x-2y)²+3(x-2y)(x+2y)

b) (y²-1)(y+2)-(y-2)(y²+2y+4)

#Toán lớp 8

Đào Lê Anh Thư

4 tháng 7 2017

a/ $\left(x-2y\right)^2+3\left(x-2y\right)\left(x+2y\right)$

$=\left(x-2y\right)\left(x-2y+3x-6y\right)=\left(x-2y\right)\left(4x-8y\right)$

$=4\left(x-2y\right)\left(x-2y\right)=4\left(x-2y\right)^2$

b/ $\left(y^2+1\right)\left(y+2\right)-\left(y+2\right)\left(y^2-2y+4\right)$

$=y^3+2y^2+y+2-y^3-8$

$=2y^2+y-6=2y^2+4y-3y-6$

$=\left(y+2\right)\left(2y-3\right)$

riêng câu b mình có sửa đề lại, bn xem có đúng hong nha. Chúc bn hc tốt nhé ^^

Đúng(0)

Trịnh Diệp

30 tháng 8 2021

(x+y/2x-2y-x-y/2x+2y-2y^2/y^2-x^2):2y/x-y

#Toán lớp 8

Nguyễn Lê Phước Thịnh

30 tháng 8 2021

Ta có: $\left(\dfrac{x+y}{2x-2y}-\dfrac{x-y}{2x+2y}-\dfrac{2y^2}{y^2-x^2}\right):\dfrac{2y}{x-y}$

$=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+4y^2}{2\left(x-y\right)\left(x+y\right)}:\dfrac{2y}{x-y}$

$=\dfrac{4y^2+4xy}{2\left(x-y\right)\left(x+y\right)}\cdot\dfrac{x-y}{2y}$

$=\dfrac{4y\left(x+y\right)}{2\left(x+y\right)\cdot2y}$

$=1$

Đúng(0)

Thanh Vân Hoàng

30 tháng 12 2020

a (2y^3-5y^2+6y-15):(2y-5) b 7/y-y/y+6+36/y^2+6y c 5x+2/3xy^2:10x+4/x^2y d 1/5x^2y(15xy^2-5y+3xy) e (x-y)(x-y)-x(x-1) Mọi người giúp e với ạ

#Toán lớp 8

Akai Haruma

Giáo viên

31 tháng 12 2020

Bạn viết đề cẩn thận bằng công thức toán thì sẽ tăng khả năng nhận được sự giúp đỡ hơn. Viết như thế này nhìn rối mắt cực.

Đúng(0)

simp luck voltia

4 tháng 1 2023

rút gọn và tính giá trị biểu thức sau tại x=-1,76và y=3/25

P=$[$($\dfrac{x-y}{2y-x}$-$\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}$):$\dfrac{4\text{x}^4+4\text{x}^2y+y^2-4}{x^2+y+xy+x}$$]$:$\dfrac{x+1}{2\text{x}^2+y+2}$

Thịnh giải hộ

#Toán lớp 8

Nguyễn Lê Phước Thịnh

5 tháng 1 2023

$=\left[\left(\dfrac{-\left(x-y\right)}{x-2y}-\dfrac{x^2+y^2+y-2}{\left(x-2y\right)\left(x+y\right)}\right):\dfrac{\left(2x^2+y\right)^2-4}{x\left(x+y\right)+\left(x+y\right)}\right]:\dfrac{x+1}{2x^2+y+2}$

$=\dfrac{-x^2+y^2-x^2-y^2-y+2}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y-2\right)\left(2x^2+y+2\right)}\cdot\dfrac{2x^2+y+2}{x+1}$

$=\dfrac{-2x^2-y+2}{\left(x-2y\right)}\cdot\dfrac{\left(x+1\right)}{\left(2x^2+y-2\right)\left(2x^2+y+2\right)}\cdot\dfrac{2x^2+y+2}{x+1}$

$=\dfrac{-1}{x-2y}$

Đúng(5)

Thầy Đức Anh

Giáo viên VIP

5 tháng 1 2023

Thay $x=-1,76$ và $y=\dfrac{3}{25}$ vào $P=\dfrac{-1}{x-2y}$, ta được:

$P=\dfrac{-1}{-1,76-2.(\dfrac{3}{25})}=\dfrac{1}{2}$.

Đúng(6)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP