Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay x=1 và y=4 vào f(x), ta được:
m-1+2m+2=4
hay m=1

\(M\left(0;1\right)\in\left(P\right)\Rightarrow c=1\)
Lại có \(I\left(-1;2\right)\) là đỉnh \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2+4a=0\\b=2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=-2\end{matrix}\right.\left(\text{Vì }a\ne0\right)\)
\(\Rightarrow y=-x^2-2x+1\)

Ta có TXĐ:D=R
⇒∀x∈D⇒−x∈D
Đồ thị hàm số đã cho nhận gốc tọa độ O làm tâm đối xứng khi và chỉ khi nó là hàm số lẻ
⇔f(−x)=−f(x),∀x∈R
\(\text{⇔(−x)^3−(m^2−9)(−x)^2+(m+3)(−x)+m−3}\)
\(\text{=-[x^3−(m^2−9)x^2+(m+3)x+m−3]}\)
\(=\text{⇔2(m^2−9)x^2−2(m−3)=0}\)
\(\Rightarrow\forall\inℝ\) ;
\(\hept{\begin{cases}m^2-9=0\\m-3=0\end{cases}}\)
\(\hept{\begin{cases}m=\pm3\\m=3\end{cases}}\)
\(\Rightarrow m=3\)

Lời giải:
\(y=mx^2-(m-2)x-2m+3\)
\(\Leftrightarrow m(x^2-x-2)+(2x+3-y)=0\)
Ta thấy điều trên luôn đúng với mọi $m$ khi và chỉ khi:
\(\left\{\begin{matrix} x^2-x-2=0\\ 2x+3-y=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (x-2)(x+1)=0\\ y=2x+3\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} (x,y)=(2,7)\\ (x,y)=(-1,1)\end{matrix}\right.\)
Vậy parabol (P) luôn đi qua 2 điểm cố định là $(2,7)$ và $(-1,1)$
Ta có đpcm.

Ta có (m – 2)x + (m – 6)y + m – 1 = 0 đúng với mọi m
⇔ mx - 2x + my - 6y + m – 1= 0 đúng với mọi m
⇔ (mx + my + m ) + ( -2x – 6y - 1)= 0 đúng với mọi m
⇔ m (x + y + 1) – (2x + 6y + 1) = 0 đúng với mọi m
Điểm cố định của d thỏa mãn
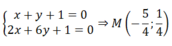
Đáp án D

a/ Để BPT vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}m+2>0\\\Delta'=m^2-3m\left(m+2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-2\\m^2+3m>0\end{matrix}\right.\) \(\Rightarrow m>0\)
b/ Để BPT vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}m+2< 0\\\Delta'\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -2\\m^2+3m\ge0\end{matrix}\right.\) \(\Rightarrow m\le-3\)
Vậy để BPT có nghiệm thì \(m>-3\)
Gọi điểm cố định của đồ thị hàm số là \(A\left(x_0;y_0\right)\)
\(\Rightarrow y_0=2mx_0+1-m\) \(\forall m\)
\(\Leftrightarrow m\left(2x_0-1\right)+1-y_0=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_0-1=0\\1-y_0=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=\frac{1}{2}\\y_0=1\end{matrix}\right.\)
\(\Rightarrow A\left(\frac{1}{2};1\right)\)