TL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 5 2017
* Với M
Ta có M= x2+y2 = x2+y2+2xy-2xy=(x+y)2 - 2xy= (-9)2 - 2.18 = 81- 36 = 45
* Với N
Ta có M = x4 + y4 = (x2)2 + (y2)2 + 2(xy)2 - 2(xy)2 = (x2+y2)2 + 2 (xy)2= 452 + 2. 182= 2673
* Với T
Ta có T = x2 - y2 => chịu
LN
14 tháng 7 2018
x^2 +y^2 =x^2 + 2xy + y^2 - 2xy
(x+y)^2 - 2xy
(-9)^2-2*18
81 - 36
45
TS
1
8 tháng 8 2017
( x+y)2= x2 +2xy+y2
=> x2 +y2 =( x+y)2 -2xy
Thay x+y =m và xy= n vào biểu thức , ta có:
x2 +y2 = m2 -2n
Vậy nếu x+y =m và xy= n thì x2 +y2 = m2 -2n.
NH
1
26 tháng 6 2017
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left[\left(x+y\right)^2-2xy\right]^2-2\left(xy\right)^2\)
\(=\left(a^2-2b\right)^2-2b^2=a^4-2.a^2.2b+4b^2-2b^2=a^4-4a^2b+2b^2\)
23 tháng 10 2021
\(P=\left(x+2y\right)^2-2\left(x+2y\right)\left(y-1\right)+\left(y-1\right)^2\\ P=\left(x+2y-y+1\right)^2=\left(x+y+1\right)^2\\ Q.sai.đề\\ M=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\\ M=1^3-3xy\left(x+y-1\right)=1-3xy\left(1-1\right)=1-0=1\\ x+y=2\Leftrightarrow\left(x+y\right)^2=4\\ \Leftrightarrow x^2+y^2+2xy=4\\ \Leftrightarrow2xy=4-10=-6\\ \Leftrightarrow xy=-3\\ N=x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\\ N=2\left(10+3\right)=2\cdot13=26\)
KN
25 tháng 7 2019
a) \(M=\left(x+y\right)^3+2x^2+4xy+2y^2\)
\(=7^3+2\left(x^2+2xy+y^2\right)\)
\(=343+2\left(x+y\right)^2\)
\(=343+2.7^2\)
\(=343+98=441\)
KN
25 tháng 7 2019
b) \(N=\left(x-y\right)^3-x^2+2xy-y^2\)
\(=\left(-5\right)^3-\left(x-y\right)^2\)
\(=-125-\left(-5\right)^2\)
\(=-125-25=-150\)
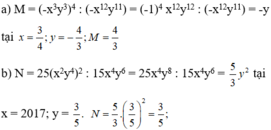
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2\)
\(=\left(m^2-2n\right)^2-2n^2=m^4-4m^2n+4n^2-2n^2=m^4-4m^2n+2n^2\)