K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
Phạm Trần Hoàng Anh
CTVHS
21 tháng 8 2020
a) 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121 x 1
= 72 x 212 + (27 + 1) x 121
= 72 x 212 + 28 x 121
= 72 x (121 + 91) + 28 x 121
= 72 x 121 + 72 x 91 + 28 x 121
= (72 + 28) x 121 + 72 x 91
= 100 x 121 + 72 x 91
= 12100 + 6552
= 18652 (anh thấy bài này sao ý)
b) (165 x 99 + 165) - ( 163 x 101 - 163)
= (165 x 99 + 165 x 1) - ( 163 x 101 - 163 x 1)
= [165 x (99 + 1)] - [163 x (101 - 1)]
= 165 x 100 - 163 x 100
= 16500 - 16300
= 200
c) 24 x 62 + 48 x 19
= 24 x 62 + (24 + 24) x 19
= 24 x 62 + 24 x 19 + 24 x 19
= 24 x (62 + 19 + 19)
= 24 x 100
= 2400
d) 24 x 76 + 48 x 12 - 20 x 100
= 24 x 76 + (24 + 24) x 12 - 20 x 100
= 24 x 76 + 24 x 12 + 24 x 12 - 20 x 100
= 24 x (76 + 12 + 12) - 20 x 100
= 24 x 100 - 20 x 100
= 100 x (24 - 20)
= 100 x 4
= 400
( nhớ tính lại xem đúng ko nha, anh lỡ có sai thì chết. Bài nào sai báo ngay cho anh )
HỌC TỐT 
H
1
1 tháng 3 2022
Gọi tử là x
Mẫu là 105-x
Theo đề, ta có:
\(\dfrac{x}{105-x}=\dfrac{60}{165}=\dfrac{4}{11}\)
=>11x=420-4x
=>15x=420
hay x=28
Vậy: Phân số cần tìm là 28/77
TN
3 tháng 3 2021
\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)
\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)
=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)
C=-1 ta được phương án A(ko tm câu hỏi)
C=0 ta được phương án B(ko tm câu hỏi)
C=2 ta được phương án C(ko tm câu hỏi)
=>chọn D
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Ý bạn là \(f(x)=\frac{1}{9+x^2}+\frac{3}{9+x^2}\) hay thế nào? Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn).
23 tháng 11 2023
1: \(2^x=64\)
=>\(x=log_264=6\)
2: \(2^x\cdot3^x\cdot5^x=7\)
=>\(\left(2\cdot3\cdot5\right)^x=7\)
=>\(30^x=7\)
=>\(x=log_{30}7\)
3: \(4^x+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+3\cdot2^x-2^x-3=0\)
=>\(\left(2^x+3\right)\left(2^x-1\right)=0\)
=>\(2^x-1=0\)
=>\(2^x=1\)
=>x=0
4: \(9^x-4\cdot3^x+3=0\)
=>\(\left(3^x\right)^2-4\cdot3^x+3=0\)
Đặt \(a=3^x\left(a>0\right)\)
Phương trình sẽ trở thành:
\(a^2-4a+3=0\)
=>(a-1)(a-3)=0
=>\(\left[{}\begin{matrix}a-1=0\\a-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\left(nhận\right)\\a=3\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3^x=1\\3^x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
5: \(3^{2\left(x+1\right)}+3^{x+1}=6\)
=>\(\left[3^{x+1}\right]^2+3^{x+1}-6=0\)
=>\(\left(3^{x+1}\right)^2+3\cdot3^{x+1}-2\cdot3^{x+1}-6=0\)
=>\(3^{x+1}\left(3^{x+1}+3\right)-2\left(3^{x+1}+3\right)=0\)
=>\(\left(3^{x+1}+3\right)\left(3^{x+1}-2\right)=0\)
=>\(3^{x+1}-2=0\)
=>\(3^{x+1}=2\)
=>\(x+1=log_32\)
=>\(x=-1+log_32\)
6: \(\left(2-\sqrt{3}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\left(\dfrac{1}{2+\sqrt{3}}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\dfrac{1}{\left(2+\sqrt{3}\right)^x}+\left(2+\sqrt{3}\right)^x=2\)
Đặt \(b=\left(2+\sqrt{3}\right)^x\left(b>0\right)\)
Phương trình sẽ trở thành:
\(\dfrac{1}{b}+b=2\)
=>\(b^2+1=2b\)
=>\(b^2-2b+1=0\)
=>(b-1)2=0
=>b-1=0
=>b=1
=>\(\left(2+\sqrt{3}\right)^x=1\)
=>x=0
7: ĐKXĐ: \(x^2+3x>0\)
=>x(x+3)>0
=>\(\left[{}\begin{matrix}x>0\\x< -3\end{matrix}\right.\)
\(log_4\left(x^2+3x\right)=1\)
=>\(x^2+3x=4^1=4\)
=>\(x^2+3x-4=0\)
=>(x+4)(x-1)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
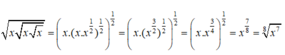
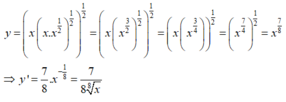
là bằng không biết