Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hình nha
a) góc ACB=góc ECN (đối đỉnh)
góc ABC=góc ACB(tam giác ABC cân )
--> góc ABC=góc ECN
xét 2 tam giác BDM và CEN có:
cạnh BD=cạnh EC(gt)
góc BDM=góc CEN(=90độ)
góc MBC=góc ECN(chứng minh trên )
--> 2 tam giác BDM=CEN(g.c.g)
--> DM=EN(2 cạnh tương ứng)
c)xét 2 tam giác AOB và AOC có:
AB=AC(tam giác ABC cân)
góc BAO=góc CAO(tia OA là p.giác của góc A)
cạnh AO chung
--> 2 tam giác AOB=AOC(c.g.c)

Bài 3 :
A B C H K I
Gọi gia điểm của các đường trung trực với AB,Ac lần lượt là H ,K
Ta có :AH + HB = AB
AK + KC = AC
mà AB = AC ( tam giác ABC cân tại A)
=> AH + HB = AK + KC
mà CH và Bk lần lượt là trung trực của AB ,AC
=> AH = HB = AK = KC
Xét tam giác AHI và tam giác AKI có
AHI = AKI = 90
AH = AK ( cmt )
AI : cạnh chung
=> tam giác AHI = tam giác AKI ( canh huyền - cạnh gosc vuông )
=> ^HAI = ^KAI ( 2 góc tương ứng )
=> AI là tia phân giác của ^A
Vậy AI là tia phân giác của ^A
Bài 1
A B C D E H K
a, Vì tam giác ABC cân tại A => AB = AC và ^ABC = ^ACB
Ta có : ^ABC + ^ABD = 180 (kề bù )
^ACB + ^ ACE = 180 ( kề bù )
mà ^ABC = ^ACB
=> ^ABD = ^ ACE
Xét tam giác ABD và tam giác ACE có :
AB =AC ( tam giác ABc cân tại a )
^ABD = ^ACE ( cmt )
BD = CE ( gt)
=> tm giác ABD = tam giác ACE ( c.g.c)
=> ^ADB = ^AEC ( 2 góc tương ứng )
hay ^HDB = ^KEC
Xét tam giác HBD và tam gisc KEC có :
^DHB = ^EKC = 90
BD = CE (gt)
HDB = KEc ( cmt )
=> tam giác HBD = tam giác KCE ( cạnh huyền - góc nhọn )
=> HB = Ck ( 2 canh tương ứng )
Vậy HB = Ck
b,Xét tam giác ABH và tam giác ACk có
AHB = AKC = 90
HB = CK ( cmt )
AB = AC
=> tam giác ABH = tam giác ACK ( anh huyền - canh góc vuồng )
Vậy tam giác ABH =tam giác ACK

1:
a: Xét ΔABD vuông tại D và ΔCAE vuông tại E có
AB=CA
góc ABD=góc CAE
=>ΔABD=ΔCAE
b: ΔABD=ΔCAE
=>BD=AE: AD=CE
=>BD-CE=BD-AD=DE

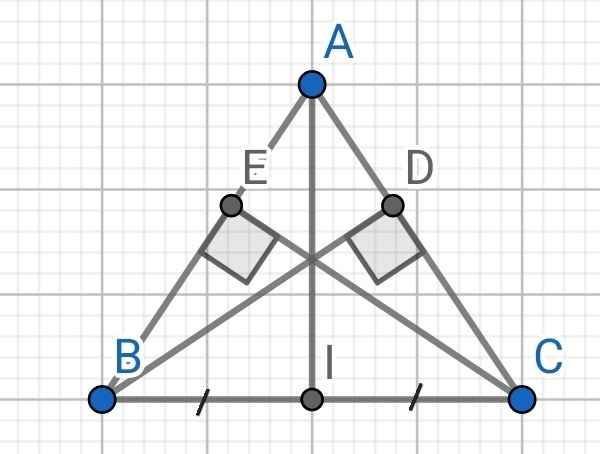 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC

c.
tg BCK: CD là đường cao
là trung tuyến
sra: tg BCK cân
sra: DBC= DKC(1)
- xét tg EBC và DCB:
BEC=BDC(=90 độ)
ABC=ACB(tg ABC cân)
BC (cạnh chung)
sra: Tg EBC= DCB(cạnh huyền-góc nhọn)
sra: ECB= DBC(cặp góc tương ứng)(2)
Từ (1) và (2)
sra: góc ECB=DKC(đfcm)

a)XÉt tam giác HBM và tam giác KCM có:
MB = Mc ( M là TĐ của BC)
góc BMH = góc CMK ( 2 góc đối đình)
MK = MH ( gt)
do đó : tam giác HBM = tam giác KCM (c-g-c)