NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
5 tháng 5 2017
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
PT
1
CM
5 tháng 12 2017
Đặt y = f(x) = |x|.
+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.
+ f(–x) = |–x| = |x| = f(x).
Vậy hàm số y = |x| là hàm số chẵn.
T
1
11 tháng 10 2021
TXĐ: D=R
Nếu \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-2\cdot\left(-x\right)^4+\left(-x\right)^2-10\)
\(=-2x^4+x^2-10\)
=f(x)
=>f(x) là hàm số chẵn
PT
1
CM
3 tháng 11 2018
Đặt y = f(x) = (x + 2)2.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ (x + 2)2 = f(x)
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ – (x + 2)2 = –f(x).
Vậy hàm số y = (x + 2)2 không chẵn, không lẻ.
PT
1
CM
16 tháng 12 2018
Đặt y = f(x) = x2 + x + 1.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
Vậy hàm số y = x2 + x + 1 không chẵn, không lẻ.
PT
1
PT
1
OM
1
20 tháng 6 2019
1. Khái niệm hàm số chẵn, hàm số lẻ
Cho hàm số y=f(x) có tập xác định D.
• Hàm số f được gọi là hàm số chẵn nếu với ∀x∈D thì −x∈D và f(x)=f(−x)
• Hàm số f được gọi là hàm số lẻ nếu với ∀x∈D thì −x∈D và f(x)=−f(−x)
Chú ý: Một hàm số có thể không chẵn cũng không lẻ.
2. Đồ thị của hàm số chẵn, hàm số lẻ
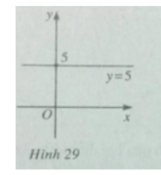
• Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
• Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
3. Phương pháp xét tính chẵn, lẻ của hàm số
Cho hàm số y=f(x)y=f(x) xác định trên DD
• f là hàm số chẵn ⇔{∀x∈D⇒−x∈Df(−x)=f(x)
• f là hàm số lẻ ⇔{∀x∈D⇒−x∈Df(−x)=−f(x)
Các bước xét tính chẵn, lẻ của hàm số:
• Bước 1. Tìm tập xác định DD của hàm số.
• Bước 2. Kiểm tra:
+ Nếu ∀x∈D⇒−x∈D∀x∈D⇒−x∈D thì chuyển qua bước 3.
+ Nếu tồn tại x0∈Dx0∈D mà −x0∉D−x0∉D thì kết luận hàm không chẵn cũng không lẻ.
• Bước 3. Xác định f(−x)f(−x) và so sánh với f(x):f(x):
+ Nếu f(−x)=f(x) thì kết luận hàm số là chẵn.
+ Nếu f(−x)=−f(x) thì kết luận hàm số là lẻ.
TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ