Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
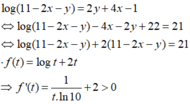
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

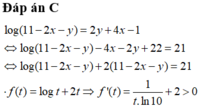
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
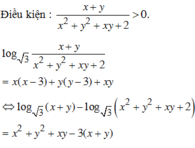
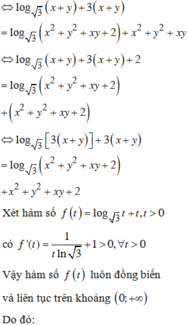
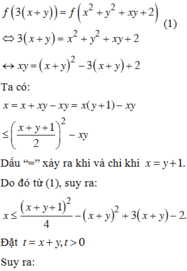
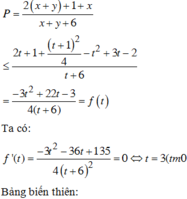
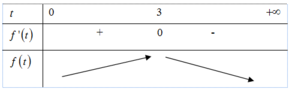



Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
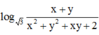
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
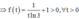
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 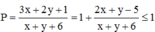
vì 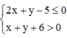
Vậy Pmax = 1 khi và chỉ khi 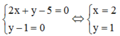
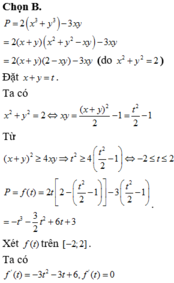
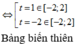






Đáp án B
Ta có P = 2 x 3 + y 3 - 3 x y = 2 x + y x 2 - x y + y 2 - 3 x y = 2 x + y 2 - x y - 3 x y
Mặt khác x 2 + y 2 = 2 ⇔ x + y 2 - 2 x y = 2 ⇔ 2 x y = x + y 2 - 2 ≤ x + y 2 2 ⇔ - 2 ≤ x + y ≤ 2
Khi đó 2 P = 2 x + y 4 - 2 x y - 6 x y = 2 x + y 4 - x + y 2 + 2 - 3 x + y 2 - 2
= 6 + 12 x + y - 3 x + y 2 - 2 x + y 3 = f t = 6 + 12 t - 3 t 2 - 2 t 3
Với t = x + y ∈ - 2 ; 2
Xét hàm số f t = 6 + 12 t - 3 t 2 - 2 t 3 trên đoạn [-2;2] ta có
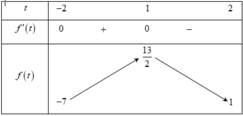
f ' t = 12 - 6 t - 6 t 2 ; f ' t = 0 ⇔ [ t = - 2 t = 1
So sánh các giá trị f(-2);f(1);f(2), ta được m a x - 2 ; 2 f t = f 1 = 13 ⇒ M = 13 2 .