K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
21 tháng 12 2018
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
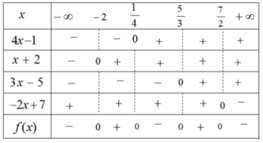
Ta có bảng xét dấu :
Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
13 tháng 1 2021
Với \(x>2\) thì f(x) > 0.
Với \(x<\frac{-3}{5}\) thì f(x) > 0.
Với \(\frac{-3}{5}< x<2\) thì f(x) < 0.
Với x = 2 thì f(x) = 0.
Với \(x=\frac{-3}{5}\) thì f(x) = 0.
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
\(f\left(x;y\right)=3x^2+y^2-2x-xy+y+3\)
\(=\left(x^2-xy+\dfrac{y^2}{4}\right)+\dfrac{1}{2}\left(4x^2-4x+1\right)+\dfrac{1}{3}\left(\dfrac{9}{4}y^2+3y+1\right)+\dfrac{13}{6}\)
\(=\left(x-\dfrac{y}{2}\right)^2+\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{3}\left(\dfrac{3y}{4}+1\right)^2+\dfrac{13}{6}>0;\forall x;y\)
NH
0