Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(x\ne1\)
\(\left(1+x+...+x^{10}\right)^{11}=a_0+a_1x+...+a_{110}x^{110}\)
\(\Leftrightarrow\left(x-1\right)^{11}\left(1+x+...+x^{10}\right)^{11}=\left(x-1\right)^{11}\left(a_1+a_1x+...+a_{110}x^{110}\right)\)
\(\Leftrightarrow\left(x^{11}-1\right)^{11}=\left(x-1\right)^{11}\left(a_0+a_1x+...+a_{110}x^{110}\right)\)
\(VP=\left(x-1\right)^{11}\left(a_0+a_1x+...\right)=\left(\sum\limits^{11}_{k=0}C_{11}^kx^k\left(-1\right)^{11-k}\right)\left(a_0+a_1x+...\right)\) (1)
Ta thấy tổng các hệ số của \(x^{11}\) trong khai triển (1) là:
\(C_{11}^0\left(-1\right)^{11}.a_{11}+C_{11}^1\left(-1\right)^{10}a_{10}+C_{11}^2\left(-1\right)^9a_9+...+C_{11}^{11}\left(-1\right)^0a_0\)
\(=-C_{11}^0a_{11}+C_{11}^1a_{10}-C_{11}^2a_9+...+C_{11}^{11}a_0=-T\)
\(VT=\sum\limits^{11}_{k=0}C_{11}^k\left(x^{11}\right)^k.\left(-1\right)^{11-k}\)
Hệ số của \(x^{11}\) trong khai triển trên là \(C_{11}^1\left(-1\right)^{10}=C_{11}^1=11\)
Mà \(VT=VP\Rightarrow-T=11\Rightarrow T=-11\)

a. Cho \(x=1\) ta được:
\(\left(1+1+2\right)^{10}=a_0+a_1+a_2+...+a_{20}\)
\(\Rightarrow S_1=4^{10}\)
b. Cho \(x=2\) ta được:
\(\left(1+2+8\right)^{10}=a_0+a_1.2+a_2.2^2+...+a_{20}.2^{20}\)
\(\Rightarrow S_2=11^{10}\)
c.
\(\left(1+x+2x^2\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x+2x^2\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i.2^ix^{i+k}\)
Số hạng chứa \(\Rightarrow\left\{{}\begin{matrix}i+k=17\\0\le i\le k\le10\end{matrix}\right.\)
\(\Rightarrow\left(i;k\right)=\left(7;10\right);\left(8;9\right)\)
\(\Rightarrow a_{17}=C_{10}^{10}C_{10}^7.2^7+C_{10}^9.C_9^8.2^8=...\)


Mình nhầm \(C^1_{2016}a_{2015}\)thành \(C^1_{2016}a^{2015}\)

Bài 1. a) trục hoành cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn
) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
b) Đường thẳng y = 1 cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ
) tại ba điểm có hoành độ ![]() . Do đó trên đoạn
. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là ![]() .
.
c) Phần phía trên trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈ ![]() .
.
d) Phần phía dưới trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈ ![]() .
.
a) \(\left\{-\pi;0;\pi\right\}\)
b) \(\left\{\dfrac{\pi}{4};\dfrac{\pi}{4}\pm\pi\right\}\)
c) \(\left(-\pi;-\dfrac{\pi}{2}\right)\cup\left(0;\dfrac{\pi}{2}\right)\cup\left(\pi;\dfrac{3\pi}{2}\right)\)
d) \(\left(-\dfrac{\pi}{2};0\right)\cup\left(\dfrac{\pi}{2};\pi\right)\)

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
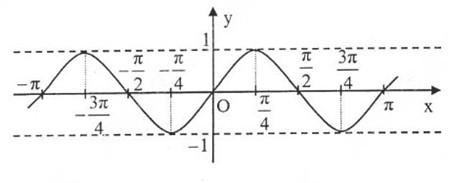
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)
