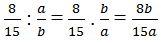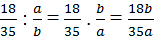Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số lớn nhất cần tìm là \(\frac{a}{b}\)
Theo đề bài thì \(\frac{8b}{15a}\) là số nguyên nên 8b \(⋮\) 15a
Mà ƯCLN(8; 15) = 1 và ƯCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta cũng có: \(\frac{18}{35}\div\frac{a}{b}=\frac{18}{35}.\frac{b}{a}=\frac{18b}{35a}\)
Tương tự 18b \(⋮\) 35a
Mà ƯCLN(18: 35) = 1 và ƯCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra:\(a\in\text{ƯC}\left(8;18\right)=\left\{0;1;2\right\}\)
\(b\in\text{ƯC}\left(15;35\right)=\left\{0;105;205;....\right\}\)
Vì \(\frac{a}{b}\)lớn nhất nên a lớn nhất, b nhỏ nhất \(\left(\ne0\right)\)
Vậy phân số cần tìm là \(\frac{2}{105}\)

Gọi số đso là a.
Để \(a:\frac{8}{15}=\frac{15a}{8}\) là số nguyên thì 15a phải chia hết cho 8. Mà ƯCLN(15;8)=1 nên a \(\in\) B(8)
Để \(a:\frac{18}{35}=\frac{35a}{18}\) là số nguyên thì 35a phải chia hết cho 18. Mà ƯCLN(35;18}=1 nên a \(\in\)B(18)
Vậy để a chia cho cả 2 phân số này ra kết quả là số nguyên thì a \(\in\) BCNN(8;18)=72
Kết luận số lớn nhất cần tìm là 72

Gọi số lớn nhất phải tìm là: \(\frac{a}{b}\)(a và b nguyên tố cùng nhau).
Ta có: \(\frac{8}{15}\):\(\frac{a}{b}\)= \(\frac{8b}{15a}\). Để \(\frac{8b}{15a}\)là số nguyên ta phải có 8b : 15a suy ra 8 : a và b : 15.
Tương tự, từ \(\frac{18}{35}\): \(\frac{a}{b}\)= \(\frac{18b}{35a}\)ta cũng suy ra 18 : a và b chia 35
Để \(\frac{a}{b}\)là số lớn nhất, ta phải có : a = UWCLN (8 ; 18) = 2 ;
b= BCNN (15 ; 35) = 105.
Phân số phải tìm là: \(\frac{2}{105}\).
Thử lại: \(\frac{8}{15}\): \(\frac{2}{105}\)= 28 ; \(\frac{18}{35}\): \(\frac{2}{105}\)= 27
Gọi số đó là a.
Để A ; 8/15 =15a/8 là số nguyên thì 15a phải chia hết cho 8. Mà ƯCLN(15;8)=1 nên a ∈ B(8)
Để a: 18 / 35 = 35a/ 18 là số nguyên thì 35a phải chia hết cho 18. Mà ƯCLN(35;18}=1 nên a ∈B(18)
Vậy để a chia cho cả 2 phân số này ra kết quả là số nguyên thì a ∈ BCNN(8;18)=72
Kết luận số lớn nhất cần tìm là 72

Bài này lớp 6 nha :
Gọi phân số cần tìm là \(\frac{a}{b}\) \(\left(b\ne0\right)\)
Ta có
Để \(\frac{8}{15}:\frac{a}{b}=\frac{8b}{15a}\in Z\) \(\Leftrightarrow b\in B\left(15\right);a\inƯ\left(8\right)\)
\(\frac{18}{35}:\frac{a}{b}=\frac{18b}{35a}\in Z\) \(\Leftrightarrow b\in B\left(35\right)\) ; a \(\in\) Ư(18)
Mà \(\frac{a}{b}\) lớn nhất nên a lớn nhất và b bé nhất <=> a = ƯCLN(8 ; 18) = 2
và b = BCNN(15 ; 35) = 105
Phân số phải tìm là \(\frac{2}{105}\)

Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105

Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b}\); \(\frac{b}{a}\)
Do phân số dương nên a;b cùng dấu hay a.b > 0
Ta có: \(\frac{a}{b}\)+ \(\frac{b}{a}\)- 2 =\(\frac{a^2+b^2-2ab}{ab}\)= \(\frac{\left(a-b\right)^2}{ab}\)> hoặc = 0
Do đó \(\frac{a}{b}\)+ \(\frac{b}{a}\) > hoặc = 2
Vậy Tổng của 1 phân sô với số nghịch đảo của nó thì không nhỏ hơn 2