
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xác suất của biến cố B là \(\dfrac{1}{6}\), vì có 6 mặt trên xúc xắc và chỉ có duy nhất một mặt là mặt 6 chấm.
b)
+ Trong trường hợp biến cố A xảy ra, xác suất của biến cố B không thay đổi. Vì hai biến cố này là độc lập, kết quả của biến cố A không ảnh hưởng đến biến cố B.
+ Trong trường hợp biến cố A không xảy ra, tức là An không gieo được mặt 6 chấm, xác suất của biến cố B là \(\dfrac{1}{6}\)
$HaNa$

Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n( Ω ) = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó A ¯ là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n ∈ ℕ )
* Ta có ![]() suy ra
suy ra ![]() Do đó
Do đó 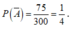
![]()

Chọn A
Có 300 số tự nhiên nhỏ hơn 300 nên n( Ω ) = 300.
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là: (297-0):3 + 1 = 100.
Số các số tự nhiên nhỏ hơn 300 mà không chia hết cho 3 là: 300 - 100 = 200 nên n(A) = 200.
Vậy 

tham khảo
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right)=0,7\)
\(\Rightarrow D\)

a) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) \Rightarrow P\left( B \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{2}{3}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{23}}{{30}}\)
b) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) = 0,5.P\left( A \right)\)
\(\begin{array}{l}P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) \Leftrightarrow 0,7 = P\left( A \right) + 0,5 - 0,5.P\left( A \right)\\ \Leftrightarrow 0,5P\left( A \right) = 0,2 \Leftrightarrow P\left( A \right) = 0,4\end{array}\)
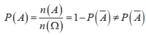

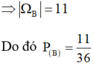
Với mỗi sự kiện đều có duy nhất một tập hợp ΩAΩA là tập hợp các kết quả thuận lợi cho sự kiện hay nói cách khác làm cho sự kiện xảy ra. Ta đồng nhất với . Khi đó chính là tập hợp các kết quả thuận lợi cho . Ta thấy là một tập con của không gian mẫu , và ta gọi là một biến cố. Như vậy mỗi tập con của không gian mẫu được gọi là một biến cố. Ta thường dùng các chữ cái in hoa để ký hiệu biến cố.
Ví dụ
Gieo con xúc sắc một lần, đây là một phép thử ngẫu nhiên với không gian mẫu , trong đó là kết quả: “Xuất hiện mặt chấm”. Xét sự kiện : “Số chấm trên mặt xuất hiện là một số chẵn”. Ta thấy rằng việc xảy ra hay không xảy ra sự kiện tùy thuộc vào kết quả của phép thử. Sự kiện xảy ra khi và chỉ khi kết quả của phép thử là 2, hoặc 4, hoặc 6. Các kết quả này được gọi là các kết quả thuận lợi cho . Gọi là tập hợp tất cả các kết quả thuận lợi cho , khi đó , đó là một tập con của .
Mỗi biến cố được đồng nhất với tập hợp tất cả các kết quả thuận lợi cho là . Do đó ta có thể viết