Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{i}=\left(1;1\right)\) nên tồn tại một số thực t sao cho \(\overrightarrow{u}=t.\overrightarrow{i}\) ⇒ \(\overrightarrow{u}=\left(t;t\right)\)
d : 3x - y - 7 = 0 nên A (2 ; - 1) ∈ d
Sau khi thực hiện phép tịnh tiến thì ta được điểm B trên d; : 3x - y + 13
thỏa mãn \(\overrightarrow{AB}=\overrightarrow{u}=\left(t;t\right)\)
⇒ B (t + 2 ; t - 1)
Do B ∉ d' ⇒ 3(t + 2) - (t - 1) + 13 = 0
⇒ t = - 10
⇒ Vecto tịnh tiến là \(\overrightarrow{u}=\left(-10;-10\right)\)

1.
Do \(\overrightarrow{v}\) cùng phương với \(\overrightarrow{u}\) nên \(\overrightarrow{v}=\left(a;a\right)\) với a là số thực khác 0
Chọn \(M\left(0;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=a+0=a\\y_{M'}=a+0=a\end{matrix}\right.\) \(\Rightarrow M'\left(a;a\right)\)
Thay vào pt d' ta được:
\(a+a-4=0\Rightarrow a=2\)
\(\Rightarrow\overrightarrow{v}=\left(2;2\right)\)
\(\Rightarrow\left|\overrightarrow{v}\right|=2\sqrt{2}\)
2.
Gọi \(\overrightarrow{u}=\left(a;b\right)\)
Gọi \(A\left(0;1\right)\) là 1 điểm thuộc d
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{u}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=a\\y_{A'}=b+1\end{matrix}\right.\)
Thay tọa độ A' vào pt d' ta được: \(a+b+1-5=0\Leftrightarrow a+b=4\)
Ta có:
\(\left|\overrightarrow{u}\right|=\sqrt{a^2+b^2}\ge\sqrt{\frac{1}{2}\left(a+b\right)^2}=2\sqrt{2}\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=2\sqrt{2}\) khi \(a=b=2\)

Độ dài bé nhất của vecto u → bằng khoảng cách từ một điểm bất kì trên d tới d’ bằng:
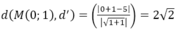
Đáp án C

Câu 2:
\(\left(x+1\right)^2+\left(y-2\right)^2=9\)
=>R=3 và I(-1;2)
Tọa độ I' là:
x=-1+1=0 và y=2-2=0
=>Phương trình (C') là: x^2+y^2=9
Câu 3:
\(V_{\left(O;-2\right)}\left(C\right)=\left(C'\right)\)
\(x^2+y^2-2x-8=0\)
=>x^2-2x+1+y^2=9
=>(x-1)^2+y^2=9
=>R=3 và I(1;0)
Tọa độ I' là:
\(\left\{{}\begin{matrix}x=1\cdot\left(-2\right)=-2\\y=0\cdot\left(-2\right)=0\end{matrix}\right.\)
Độ dài R' là:
\(R=3\cdot\left|-2\right|=6\)
Tọa độ (C') là:
\(\left(x+2\right)^2+y^2=36\)

trường hợp trùng nhau : nếu vecto u là vecto chỉ phương của d'
trườn hợp song song : nếu vecto u không là vecto chỉ phương của d'
Không bao giờ cắt nhau