Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì \(-6< 0\)nên hàm số (1) là hàm nghịch biến
Vì \(A\left(-1;6\right)\in\left(1\right)\)
\(\Rightarrow6=\left(-6\right).\left(-1\right)+m-1\)
\(\Leftrightarrow6=6+m-1\)
\(\Leftrightarrow m=1\)
b, Đths (1) cắt đths 2 tại 1 điểm trên trục tung nên
\(\hept{\begin{cases}m-1\ne3m-11\\x=0\\-6x+m-1=\left(m-1\right)x+3m-11\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m-1\ne3m-11\\m-1=3m-11\end{cases}}\)ko tìm đc m

Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1

Lời giải:
Vì đths đi qua điểm $A(1;2)$ nên:
$y_A=(m-1)x_A^2$
$\Leftrightarrow 2=(m-1).1^2$
$\Leftrightarrow m-1=2\Leftrightarrow m=3$
b. ĐTHS tìm được: $y=2x^2$ (dễ dàng tự vẽ)

Đồ thị hàm số đi qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: 2 = a - 1 2 } ⇔ a = 2
Hàm số đã cho: y = 2 x 2
Vẽ đồ thị hàm số: y = 2 x 2
x |
-2 |
-1 |
0 |
1 |
2 |
| y = 2 x 2 | 8 |
2 |
0 |
2 |
8 |
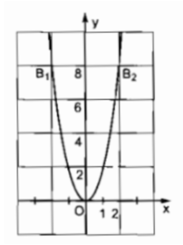

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 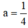
Vậy hàm số: 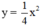
| x | -4 | -2 | 0 | 2 | 4 |
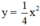 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
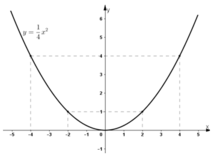

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 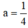
Vậy hàm số: 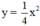
| x | -4 | -2 | 0 | 2 | 4 |
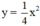 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:

a. để hàm số đi qua M(-1,1) thì ta có
\(1=\left(2m-1\right)\times\left(-1\right)+m+1\Leftrightarrow m=1\)
b.Hàm số cắt trụ tung tại điểm \(A\left(0,m+1\right)\)
Hàm số cắt trục hoành tại điểm \(B\left(\frac{-m-1}{2m-1},0\right)\)
Để OAB là tam giác cân thì ta có \(OA=OB\ne0\Leftrightarrow\left|m+1\right|=\left|\frac{-m-1}{2m-1}\right|\ne0\)
\(\Leftrightarrow\left|2m-1\right|=1\Leftrightarrow\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
a, Để đồ thị đi qua điểm M(-1;1) thì ta thay x = -1, y = 1 vào hàm số ta có:
\(1=\left(2m-1\right).\left(-1\right)+m+1\)
=>\(m=1\)
b,\(y=\left(2m-1\right)x+m+1\)
Cho \(x=0=>y=m+1=>OA=|m+1|\)
Cho \(y=0=>x=\frac{-m-1}{2m-1}=>B\left(\frac{-m-1}{2m-1};0\right)\)
\(=>OB=|\frac{-m-1}{2m-1}|=\frac{|m+1|}{|2m-1|}\)
\(\Delta AOB\)cân \(< =>\hept{\begin{cases}OA=OB\\OA>0\end{cases}}< =>\hept{\begin{cases}|m+1|\\|m+1|>0\end{cases}}\)
\(\hept{\begin{cases}|2m-1|\\m\ne-1\end{cases}< =>\hept{\begin{cases}2m-1=1\\2m-1=-1\end{cases}}}< =>\hept{\begin{cases}m=1\\m=0\end{cases}}\)
Vậy với m = 0 hoặc m = 1 thì đồ thị hàm số thỏa mãn yêu cầu của bài toán

em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.
Vì đồ thị hàm số y=(3m-2)x+5-n đi qua A(1;-2) và B(-2;9) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3m-2+5-n=-2\\-2\left(3m-2\right)+5-n=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3m-n=-5\\-6m+4+5-n=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-n=-5\\-6m-n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9n=-5\\-6m=n\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{-5}{9}\\-6m=\dfrac{-5}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{-5}{9}\\m=\dfrac{5}{54}\end{matrix}\right.\)
Vậy: Hàm số cần tìm là \(y=\dfrac{-31}{18}x+\dfrac{50}{9}\)