
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Để \(y=\left(a-4\right)x+5//y=3x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-4=3\\5\ne2\end{matrix}\right.\Leftrightarrow a=7\)
b, Thay \(x=2;y=-4\Leftrightarrow-4=2a+b\)
Thay \(x=-1;y=5\Leftrightarrow-a+b=5\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=-4\\b-a=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)

Đồ thị hàm số y = ax + b đi qua A(-4; -2) ⇔ a.(-4) + b = -2
Đồ thị hàm số y = ax + b đi qua B(2 ; 1) ⇔ a.2 + b = 1
Ta có hệ phương trình :
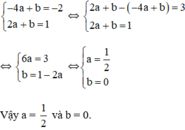

Đáp án B
Do đồ thị hàm số đã cho đi qua hai điểm A và B nên ta có:
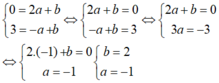

a) Hệ số góc bằng 2
=> a=2
Đồ thị hàm số đi qua A (1; 2)
=> 2=a.1+b<=> 2=2.1+b <=> b=0
Vậy hàm số: y=2x
b)
+) Đồ thị hàm số đi qua điểm A (-2; 2)
=> 2=a. (-2)+b <=> -2a+b=2 (1)
+) Đồ thị hàm số cắt đường thẳng (d) y=-2x+4 tại điểm có hoành độ bằng 3
Gọi điểm đó là: B(3; y)
(d) qua B(3; y) => y=-2.3+4=-2
=> B(3; -2)
đồ thị hàm số qua B => -2=a.3+b <=> 3a+b=-2 (2)
Từ (1); (2) ta có:a=-4/5, b=2/5
Vậy: y=-4/5 x+2/5

Đồ thị qua \(A\left(1;-1\right)\) \(\Rightarrow-1=a.1+b\Rightarrow-a-b=1\left(1\right)\)
Đồ thị qua \(B\left(2;1\right)\Rightarrow1=a.2+b\Rightarrow-2a-b=-1\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=2\\b=-3\end{matrix}\right.\)
Vậy hàm số có dạng \(y=2x-3\)