K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1

YN
28 tháng 4 2022
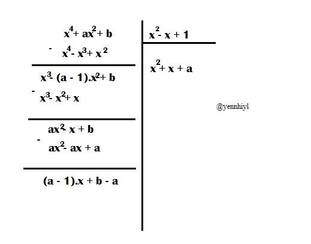
Phần dư của phép chia là \(R=\left(a-1\right).x+b-a\)
Để phép chia trên là phép chia hết thì \(R=0\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b-a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b-1=0\end{matrix}\right.\Leftrightarrow a=b=1\)
H
2

VK
28 tháng 10 2018
Đen đủi mất cái nikl àm giúp mk với
mk mới chỉ hk chia đa thức thôi chứ chưa hk định lí gì gì đó.

5 tháng 2 2022
a: \(\Leftrightarrow10x^2-15x+8x-12+a+12⋮2x-3\)
=>a+12=0
hay a=-12
b: \(\Leftrightarrow2x^2+8x+\left(a-8\right)x+4a-32-4a+28⋮x+4\)
=>-4a+28=0
=>a=7
c: \(\Leftrightarrow2x^3-2x-x^2+1+\left(a+2\right)x+b-1⋮x^2-1\)
=>a+2=0 và b-1=0
=>a=-2 và b=1
a) Đặt \(f\left(x\right)=x^4+ax+b\text{⋮}x^2-4=\left(x+2\right)\left(x-2\right)\)
Áp dụng định lý Bê du có :
\(f\left(2\right)=f\left(-2\right)=0\)
\(\Rightarrow2^4+\left(-2\right).a+b=\left(-2\right)^4+2a+b\)
\(\Leftrightarrow a=0\)
Do đó \(\hept{\begin{cases}a=0\\b\in R\end{cases}}\)
Vậy ...
b) Mình không làm được :) Mình sẽ hỏi cô mình và trả lời cho bạn sau.
a/ Đặt \(f\left(x\right)=x^4+ax+b=\left(x-2\right)\left(x+2\right).Q\left(x\right)\)với Q(x) là đa thức thương
Suy ra : \(\hept{\begin{cases}f\left(2\right)=16+2a+b=0\\f\left(-2\right)=16-2a+b=0\end{cases}}\) \(\Rightarrow\hept{\begin{cases}2a+b=-16\\-2a+b=-16\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=0\\b=-16\end{cases}}\)
b/ Ta có \(x^4+4=\left(x^4+4x^2+4\right)-4x^2=\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2+2x+2\right)\left(x^2-2x+2\right)\)
Vậy \(x^2+ax+b\) sẽ có một trong hai dạng : \(x^2+ax+b=x^2+2x+2\Rightarrow\hept{\begin{cases}a=2\\b=2\end{cases}}\)
hoặc \(x^2+ax+b=x^2-2x+2\Rightarrow\hept{\begin{cases}a=-2\\b=2\end{cases}}\)