
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{6}=\dfrac{x+y}{3+6}=\dfrac{90}{9}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10\cdot3=30\\y=10\cdot6=60\end{matrix}\right.\)
Vậy ...
b/Ta có:
\(\dfrac{x}{3}=\dfrac{4x}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{4x}{12}=\dfrac{y}{6}=\dfrac{4x-y}{12-6}=\dfrac{42}{6}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\cdot3=21\\y=7\cdot6=42\end{matrix}\right.\)
Vậy ...
c/Đặt \(x=k;y=k\) ( k \(\in\) N* )
\(\Rightarrow x=3k;=6k\)
Mà \(xy=162\)
\(\Rightarrow3k\cdot6k=162\)
\(\Rightarrow18k^2=162\)
\(\Rightarrow k^2=9\)
\(\Rightarrow k=\pm3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\cdot3=9\\x=\left(-3\right)\cdot3=-9\\y=3\cdot6=18\\y=\left(-3\right)\cdot6=-18\end{matrix}\right.\)
Vậy ...
#NoSimp

i) Ta có: \(\frac{x}{3}=\frac{y}{6}.\)
=> \(\frac{x}{3}=\frac{y}{6}\) và \(x+y=90.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{3}=\frac{y}{6}=\frac{x+y}{3+6}=\frac{90}{9}=10.\)
\(\left\{{}\begin{matrix}\frac{x}{3}=10\Rightarrow x=10.3=30\\\frac{y}{6}=10\Rightarrow y=10.6=60\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(30;60\right).\)
ii) Ta có: \(\frac{x}{3}=\frac{y}{6}.\)
=> \(\frac{4x}{12}=\frac{y}{6}\) và \(4x-y=42.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{4x}{12}=\frac{y}{6}=\frac{4x-y}{12-6}=\frac{42}{6}=7.\)
\(\left\{{}\begin{matrix}\frac{x}{3}=7\Rightarrow x=7.3=21\\\frac{y}{6}=7\Rightarrow y=7.6=42\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(21;42\right).\)
Chúc bạn học tốt!

c, Ta có: \(\frac{x}{3}=\frac{y}{6}\) và \(4x-y=42\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{6}=\frac{4x-y}{12-6}=\frac{42}{6}=7\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{x}{3}=7\Rightarrow x=7.3=21\\\frac{y}{6}=7\Rightarrow y=7.6=42\end{matrix}\right.\)
Vậy \(x=21\) và \(y=42\)
# Băng


đặt x/3=y/4=k
=>x=3k
y=4k
=>xy=3k.4k=12.k^2 =300
=>k^2 =25
=>k=5
=>x=5.3=15
y=5.4=20
b)chờ chút
a, ta co\(\frac{x}{3}=\frac{y}{4}=>\frac{x^2}{9}=\frac{x}{3}.\frac{y}{4}=\)\(\frac{300}{12}=25\)
=> x= 15=> y=10

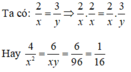
⇒ x2 = 64
⇒ x = 8 hoặc x = -8
Nếu x = 8 thì y = 96 : 8 = 12.
Nếu x = -8 thì y = 96 : (-8) = -12.

Đặt \(\dfrac{x}{3}=\dfrac{y}{6}=k\Rightarrow x=3k;y=6k\)
\(xy=162\\ \Rightarrow18k^2=162\\ \Rightarrow k^2=9\\ \Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=9;y=18\\x=-9;y=-18\end{matrix}\right.\)
Ta có:\(\dfrac{x}{3}=\dfrac{y}{6}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=3k\\y=6k\end{matrix}\right.\)
mà \(x.y=162\)
\(\Rightarrow3k.6k=162\)
\(\Rightarrow18k^2=162\)
\(\Rightarrow k=3\)
\(\Rightarrow\left\{{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{6}=3\\\dfrac{x}{3}=\dfrac{y}{6}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=9;y=18\\x=-9;y=-18\end{matrix}\right.\)

a)
\(5x=7y\Rightarrow\frac{x}{7}=\frac{y}{5}\) và x+2y=51
áp dụng t/c dãy tỷ số = nhau ta có:
\(\frac{x}{7}=\frac{y}{5}=\frac{x+2y}{7+10}=\frac{51}{17}=3\)
\(\Rightarrow\frac{x}{7}=3\Rightarrow x=3.7=21\)
\(\Rightarrow\frac{y}{5}=3\Rightarrow y=3.5=15\)

Ta có: \(\dfrac{x}{3}=\dfrac{y}{6}\Rightarrow x=\dfrac{3y}{6}=\dfrac{1}{2}y\)
Theo đề bài ta có : \(xy=162\Rightarrow\dfrac{1}{2}y.y=162\Rightarrow y^2=324\Rightarrow y=18\)
\(\Rightarrow x=\dfrac{1}{2}y=9\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{6}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=6k\end{matrix}\right.\)
Ta có: xy=162
\(\Leftrightarrow18k^2=162\)
\(\Leftrightarrow k^2=9\)
Trường hợp 1: k=3
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=9\\y=6k=18\end{matrix}\right.\)
Trường hợp 2: k=-3
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-9\\y=6k=-18\end{matrix}\right.\)

\(\text{Đ}\text{ặt}:\frac{x}{3}=\frac{y}{6}=k\)
\(\Rightarrow\hept{\begin{cases}x=3k\\y=6k\end{cases}}\)
\(xy=162\)
\(\Rightarrow3k.6k=162\)
\(18k^2=162\)
\(k^2=9\)
\(k=\pm3\)
\(\Rightarrow\hept{\begin{cases}x=\pm9\\y=\pm18\end{cases}}\)