Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{x-1}=5-\sqrt{x-4}$
$\Rightarrow x-1=25+x-4-10\sqrt{x-4}$
$\Leftrightarrow 22=10\sqrt{x-4}$
$\Leftrightarrow 2,2=\sqrt{x-4}$
$\Leftrightarrow 4,84=x-4\Leftrightarrow x=8,84$
(thỏa mãn)
2. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow (2x-2\sqrt{x})-(5\sqrt{x}-5)=0$
$\Leftrightarrow 2\sqrt{x}(\sqrt{x}-1)-5(\sqrt{x}-1)=0$
$\Leftrightarrow (\sqrt{x}-1)(2\sqrt{x}-5)=0$
$\Leftrightarrow \sqrt{x}-1=0$ hoặc $2\sqrt{x}-5=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{25}{4}$ (tm)
3. ĐKXĐ: $x\geq 3$
Bình phương 2 vế thu được:
$3x-2+2\sqrt{(2x+1)(x-3)}=4x$
$\Leftrightarrow 2\sqrt{(2x+1)(x-3)}=x+2$
$\Leftrightarrow 4(2x+1)(x-3)=(x+2)^2$
$\Leftrightarrow 4(2x^2-5x-3)=x^2+4x+4$
$\Leftrightarrow 7x^2-24x-16=0$
$\Leftrightarrow (x-4)(7x+4)=0$
Do $x\geq 3$ nên $x=4$
Thử lại thấy thỏa mãn
Vậy $x=4$
√(x² + x + 1) = 1
⇔ x² + x + 1 = 1
⇔ x² + x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0
*) x + 1 = 0
⇔ x = -1
Vậy x = 0; x = -1
--------------------
√(x² + 1) = -3
Do x² ≥ 0 với mọi x
⇒ x² + 1 > 0 với mọi x
⇒ x² + 1 = -3 là vô lý
Vậy không tìm được x thỏa mãn yêu cầu
--------------------
√(x² - 10x + 25) = 7 - 2x
⇔ √(x - 5)² = 7 - 2x
⇔ |x - 5| = 7 - 2x (1)
*) Với x ≥ 5, ta có
(1) ⇔ x - 5 = 7 - 2x
⇔ x + 2x = 7 + 5
⇔ 3x = 12
⇔ x = 4 (loại)
*) Với x < 5, ta có:
(1) ⇔ 5 - x = 7 - 2x
⇔ -x + 2x = 7 - 5
⇔ x = 2 (nhận)
Vậy x = 2
--------------------
√(2x + 5) = 5
⇔ 2x + 5 = 25
⇔ 2x = 20
⇔ x = 20 : 2
⇔ x = 10
Vậy x = 10
-------------------
√(x² - 4x + 4) - 2x +5 = 0
⇔ √(x - 2)² - 2x + 5 = 0
⇔ |x - 2| - 2x + 5 = 0 (2)
*) Với x ≥ 2, ta có:
(2) ⇔ x - 2 - 2x + 5 = 0
⇔ -x + 3 = 0
⇔ x = 3 (nhận)
*) Với x < 2, ta có:
(2) ⇔ 2 - x - 2x + 5 = 0
⇔ -3x + 7 = 0
⇔ 3x = 7
⇔ x = 7/3 (loại)
Vậy x = 3
1)
\(\Leftrightarrow x^2+x+1=1^2=1\\ \Leftrightarrow x^2+x=0\\ \Leftrightarrow x\left(x+1\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
2) Do \(x^2+1>0\forall x\) nên \(x\in\varnothing\)
3)
\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=7-2x\\ \Leftrightarrow\left|x-5\right|=7-2x\)
Nếu \(x\ge5\) thì
\(\Leftrightarrow x-5-7+2x=0\\ \Leftrightarrow3x-12=0\\ \Leftrightarrow3x=12\\ \Rightarrow x=4\)
=> Loại trường hợp này
Nếu \(x< 5\) thì
\(\Leftrightarrow5-x-7+2x=0\\ \Leftrightarrow x-2=0\\ \Rightarrow x=2\)
=> Nhận trường hợp này
Vậy x = 2
4)
\(\Leftrightarrow2x+5=5^2=25\\ \Leftrightarrow2x=25-5=20\\ \Rightarrow x=\dfrac{20}{2}=10\)
5)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\\ \Leftrightarrow\left|x-2\right|-2x+5=0\)
Nếu \(x\ge2\) thì
\(\Leftrightarrow x-2-2x+5=0\\ \Leftrightarrow3-x=0\\ \Rightarrow x=3\)
=> Nhận trường hợp này
Nếu \(x< 2\) thì
\(\Leftrightarrow2-x-2x+5=0\\ \Leftrightarrow7-3x=0\\ \Leftrightarrow3x=7\\ \Rightarrow x=\dfrac{7}{3}\)
=> Loại trường hợp này
Vậy x = 3
`a)sqrt{x^2-2x+1}=2`
`<=>sqrt{(x-1)^2}=2`
`<=>|x-1|=2`
`**x-1=2<=>x=3`
`**x-1=-1<=>x=-1`.
Vậy `S={3,-1}`
`b)sqrt{x^2-1}=x`
Điều kiện:\(\begin{cases}x^2-1 \ge 0\\x \ge 0\\\end{cases}\)
`<=>` \(\begin{cases}x^2 \ge 1\\x \ge 0\\\end{cases}\)
`<=>x>=1`
`pt<=>x^2-1=x^2`
`<=>-1=0` vô lý
Vậy pt vô nghiệm
`c)sqrt{4x-20}+3sqrt{(x-5)/9}-1/3sqrt{9x-45}=4(x>=5)`
`pt<=>sqrt{4(x-5)}+sqrt{9*(x-5)/9}-sqrt{(9x-45)*1/9}=4`
`<=>2sqrt{x-5}+sqrt{x-5}-sqrt{x-5}=4`
`<=>2sqrt{x-5}=4`
`<=>sqrt{x-5}=2`
`<=>x-5=4`
`<=>x=9(tmđk)`
Vậy `S={9}.`
`d)x-5sqrt{x-2}=-2(x>=2)`
`<=>x-2-5sqrt{x-2}+4=0`
Đặt `a=sqrt{x-2}`
`pt<=>a^2-5a+4=0`
`<=>a_1=1,a_2=4`
`<=>sqrt{x-2}=1,sqrt{x-2}=4`
`<=>x_1=3,x_2=18`,
`e)2x-3sqrt{2x-1}-5=0`
`<=>2x-1-3sqrt{2x-1}-4=0`
Đặt `a=sqrt{2x-1}(a>=0)`
`pt<=>a^2-3a-4=0`
`a-b+c=0`
`<=>a_1=-1(l),a_2=4(tm)`
`<=>sqrt{2x-1}=4`
`<=>2x-1=16`
`<=>x=17/2(tm)`
Vậy `S={17/2}`
d.
ĐKXĐ: $x\geq 2$. Đặt $\sqrt{x-2}=a(a\geq 0)$ thì pt trở thành:
$a^2+2-5a=-2$
$\Leftrightarrow a^2-5a+4=0$
$\Leftrightarrow (a-1)(a-4)=0$
$\Rightarrow a=1$ hoặc $a=4$
$\Leftrightarrow \sqrt{x-2}=1$ hoặc $\sqrt{x-2}=4$
$\Leftrightarrow x=3$ hoặc $x=18$ (đều thỏa mãn)
e. ĐKXĐ: $x\geq \frac{1}{2}$
Đặt $\sqrt{2x-1}=a(a\geq 0)$ thì pt trở thành:
$a^2+1-3a-5=0$
$\Leftrightarrow a^2-3a-4=0$
$\Leftrightarrow (a+1)(a-4)=0$
Vì $a\geq 0$ nên $a=4$
$\Leftrightarrow \sqrt{2x-1}=4$
$\Leftrightarrow x=\frac{17}{2}$
1.
$x+3+\sqrt{x^2-6x+9}=x+3+\sqrt{(x-3)^2}=x+3+|x-3|$
$=x+3+(3-x)=6$
2.
$\sqrt{x^2+4x+4}-\sqrt{x^2}=\sqrt{(x+2)^2}-\sqrt{x^2}$
$=|x+2|-|x|=x+2-(-x)=2x+2$
3.
$\sqrt{x^2+2\sqrt{x^2-1}}-\sqrt{x^2-2\sqrt{x^2-1}}$
$=\sqrt{(\sqrt{x^2-1}+1)^2}-\sqrt{(\sqrt{x^2-1}-1)^2}$
$=|\sqrt{x^2-1}+1|+|\sqrt{x^2-1}-1|$
$=\sqrt{x^2-1}+1+|\sqrt{x^2-1}-1|$
4.
$\frac{\sqrt{x^2-2x+1}}{x-1}=\frac{\sqrt{(x-1)^2}}{x-1}$
$=\frac{|x-1|}{x-1}=\frac{x-1}{x-1}=1$
5.
$|x-2|+\frac{\sqrt{x^2-4x+4}}{x-2}=2-x+\frac{\sqrt{(x-2)^2}}{x-2}$
$=2-x+\frac{|x-2|}{x-2}|=2-x+\frac{2-x}{x-2}=2-x+(-1)=1-x$
6.
$2x-1-\frac{\sqrt{x^2-10x+25}}{x-5}=2x-1-\frac{\sqrt{(x-5)^2}}{x-5}$
$=2x-1-\frac{|x-5|}{x-5}$
a: ta có: \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\)
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow\sqrt{x-1}=1\)
hay x=2
c: Ta có: \(\sqrt{1-2x^2}=x-1\)
\(\Leftrightarrow1-2x^2=x^2-2x+1\)
\(\Leftrightarrow-3x^2+2x=0\)
\(\Leftrightarrow-x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)
a, ĐKXĐ: \(x^2-4x+4\ge0\Rightarrow\left(x-2\right)^2\ge0\left(luônđúng\right)\)
\(\sqrt{x^2-4x+4}=1\\ \Rightarrow x-2=1\\ \Rightarrow x=3\)
b,\(ĐKXĐ:1-4x+4x^2\ge0\Rightarrow\left(1-2x\right)^2\ge0\left(luônđúng\right)\)
\(\sqrt{1-4x+4x^2}=5\\ \Rightarrow\left|1-2x\right|=5\\ \Rightarrow\left[{}\begin{matrix}1-2x=5\\1-2x=-5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
d, ĐKXĐ: \(\left\{{}\begin{matrix}9x^2\ge0\\2x+1\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ge-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x\ge0\)
\(\sqrt{9x^2}=2x+1\\ \Rightarrow\left|3x\right|=2x+1\\ \Rightarrow\left[{}\begin{matrix}3x=2x+1\\3x=-2x+1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)
c, ĐKXĐ: \(1-2x+x^2\ge0\Rightarrow\left(1-x\right)^2\ge0\left(luônđúng\right)\)
\(\sqrt{1-2x+x^2}-6=0\\ \Rightarrow\left|1-x\right|=6\\ \Rightarrow\left[{}\begin{matrix}1-x=-6\\1-x=6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)
e, \(\left\{{}\begin{matrix}9-6x+x^2\ge0\\x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left(3-x\right)^2\ge0\left(luônđúng\right)\\x\ge0\end{matrix}\right.\)\(\Rightarrow x\ge0\)
\(\sqrt{9-6x+x^2}=x\\ \Rightarrow\left|3-x\right|=x\\ \Rightarrow\left[{}\begin{matrix}3-x=-x\\3-x=x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3=0\left(vôlí\right)\\x=1,5\end{matrix}\right.\)
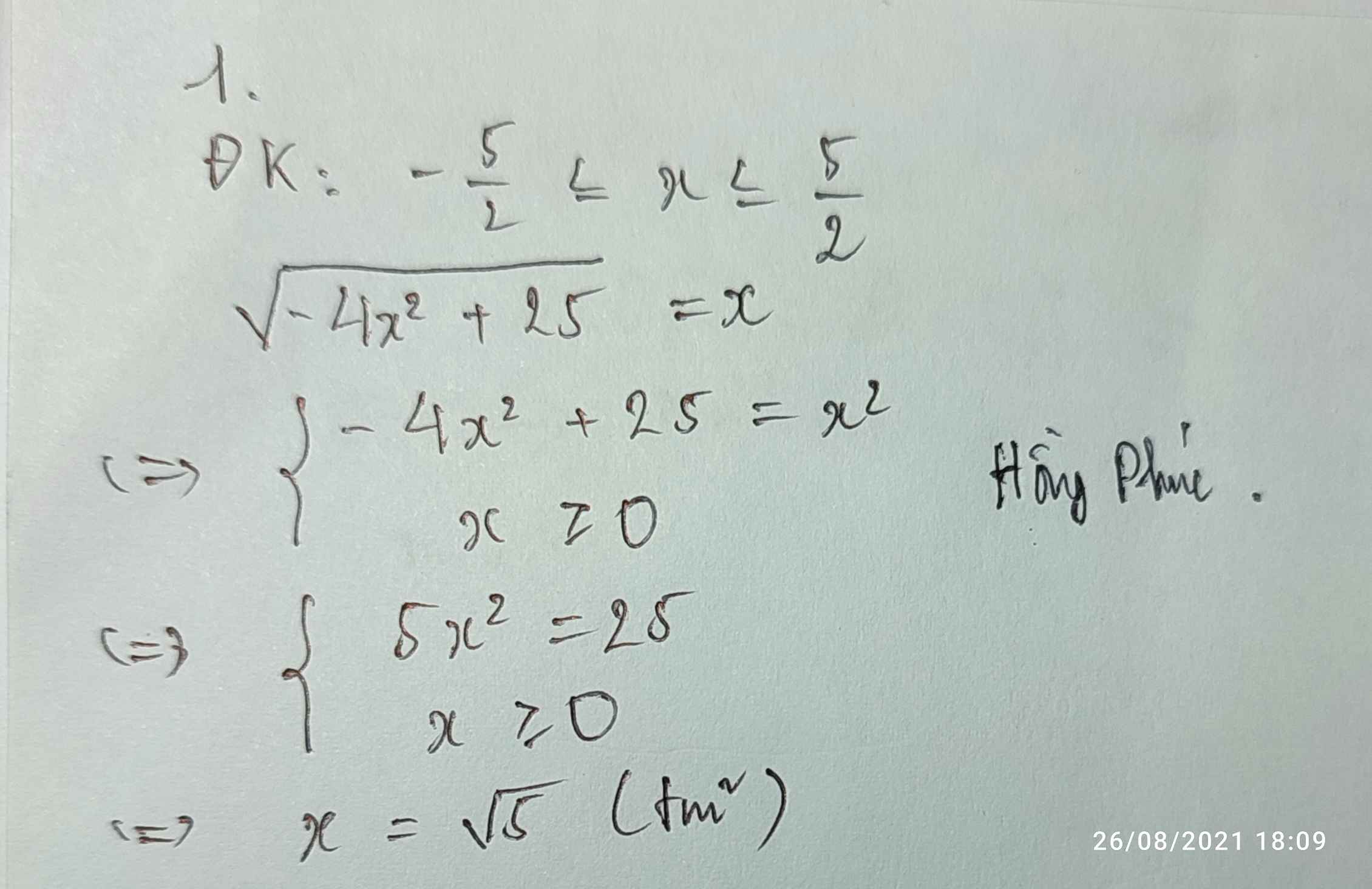
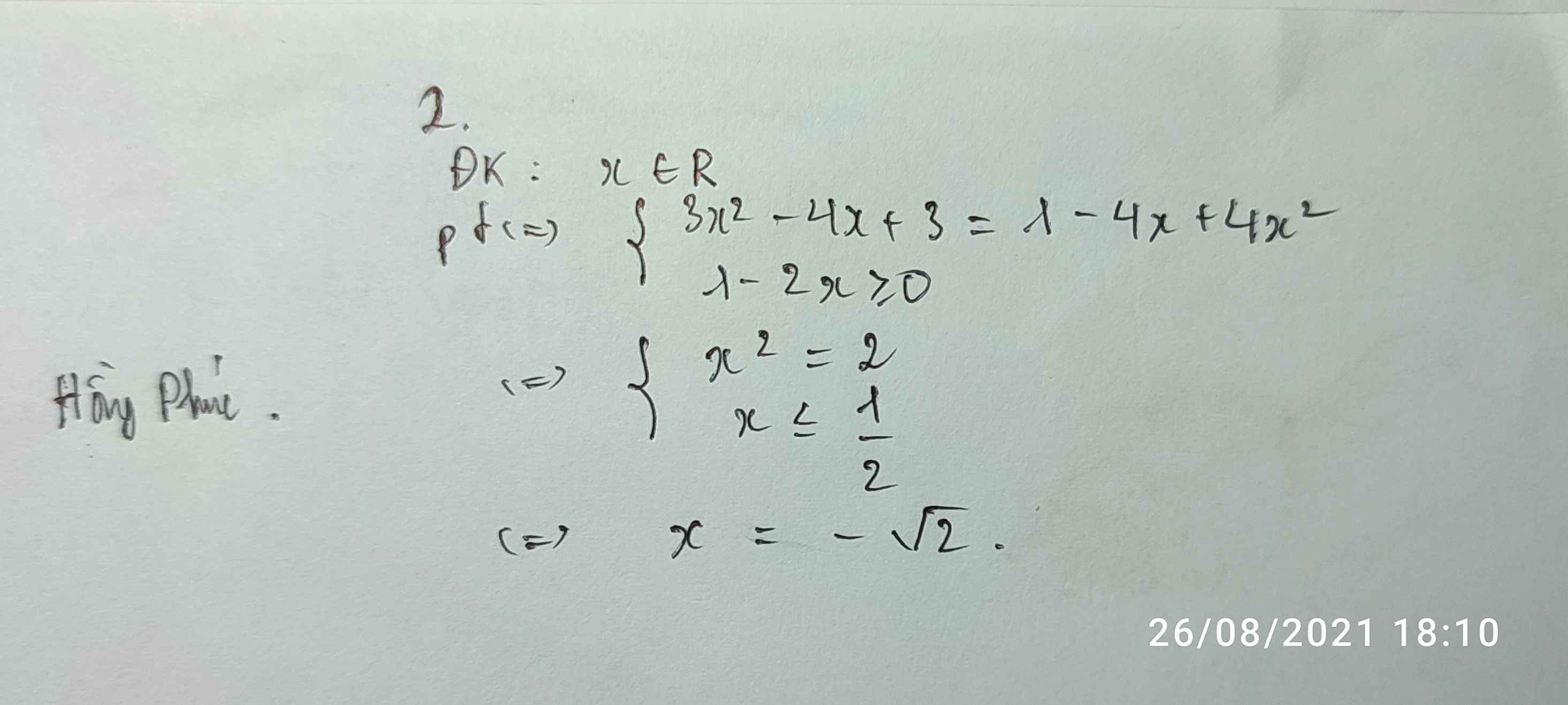
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề và hỗ trợ bạn nhanh hơn nhé.