Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

|-3|-[(-5)^3.10+(15+26):3^2]
=3-[-125.10+41:9]=3-[-1250+41/9]=3-(-11201/9)=-11198/9

a) 52x+1=125
=>52x+1= 53
=>2x+1=3
=>2x = 2
=>x =1
c)73<x <=93
=>343<x<=729
=> x = { 344;345;...;729}
d) (2x+3)4=81
=>(2x+3)4=34
=>2x+3 =3
=>2x =0
=> x = 0
nhớ tk nha
a)52x+1=125
52x+1=53
⏩ 2x+1=3
2x=4
x=4:2
x=2
b) (2x)2(2x) 3 =25.25
(2x) 2 (2x) 3 =210
(2x) 5=1024
(2x) 5 =45
2x=4
x=4 :2=2
d)(2x +3)4=81
(2x +3)4=34
2x+3=3
2x=0
x=0
Câu c bạn tự giải nhé
Nhớ tk giùm mình đấy

a, -(-46 + 54 - 37) + (-95 + 15 +64)
=46 - 54 +37 -95 +15+64
=13
b,(-3)^2 + 3^2 - (-3)^0
=9 + 9 - 1
=17
k mình nha. mình nhanh nhất

b2
P=4a^2 + 4a =4(a^2 + a)=4.[a.a + a]=4[a.(a+1)]
Mà a và a+1 là 2 số nguyên liên tiếp nên tích 2 số này chia hết cho 2
Đặt a(a+1)=2.k ( k thuộc Z)
Suy ra: P=4.2k=8k chia hết cho 8
k ch mình nha

\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)

D= 1x1x2x2x3x3x4x4x...x100x100
D= (1x2x3x4x...x100) x (1x2x3x4x...x100)
D=(1x2x3x4x...x100)2

Phải vì 23=8 chia hết cho 8 => chia hêt cho 4
52=25 chia hết cho 25
13 chia hết cho 13
Vì chia hết cho 4 và chia hết cho 5 => chia hết cho 40

Ta có :A= (1+2)+(22+23+24)+..........+(22015+22016+22017)
A= 3.22.(1+2+22)+.......+22015.(1+2+22)
A=3.22.7+........+22015.7
A=3+7.(22+.....+22015)
A= 7.(22+....+22015) +3
Vậy A chia có dư r=3
A = 1 + 2 + 22 +......+ 22016 + 22017
= (1 + 2) + (22 + 23 + 24) + (25 + 26 + 27) + ...... + (22015 + 22016 + 22017)
= 3 + 22(1 + 2 + 22) + 25(1 + 2 + 22) + .... + 22015(1 + 2 + 22)
= 3 + 7(22 + 25 +....+ 22015)
Ta thấy 7(22 + 25 +....+ 22015) \(⋮7\)
Vậy A chia 7 dư 3
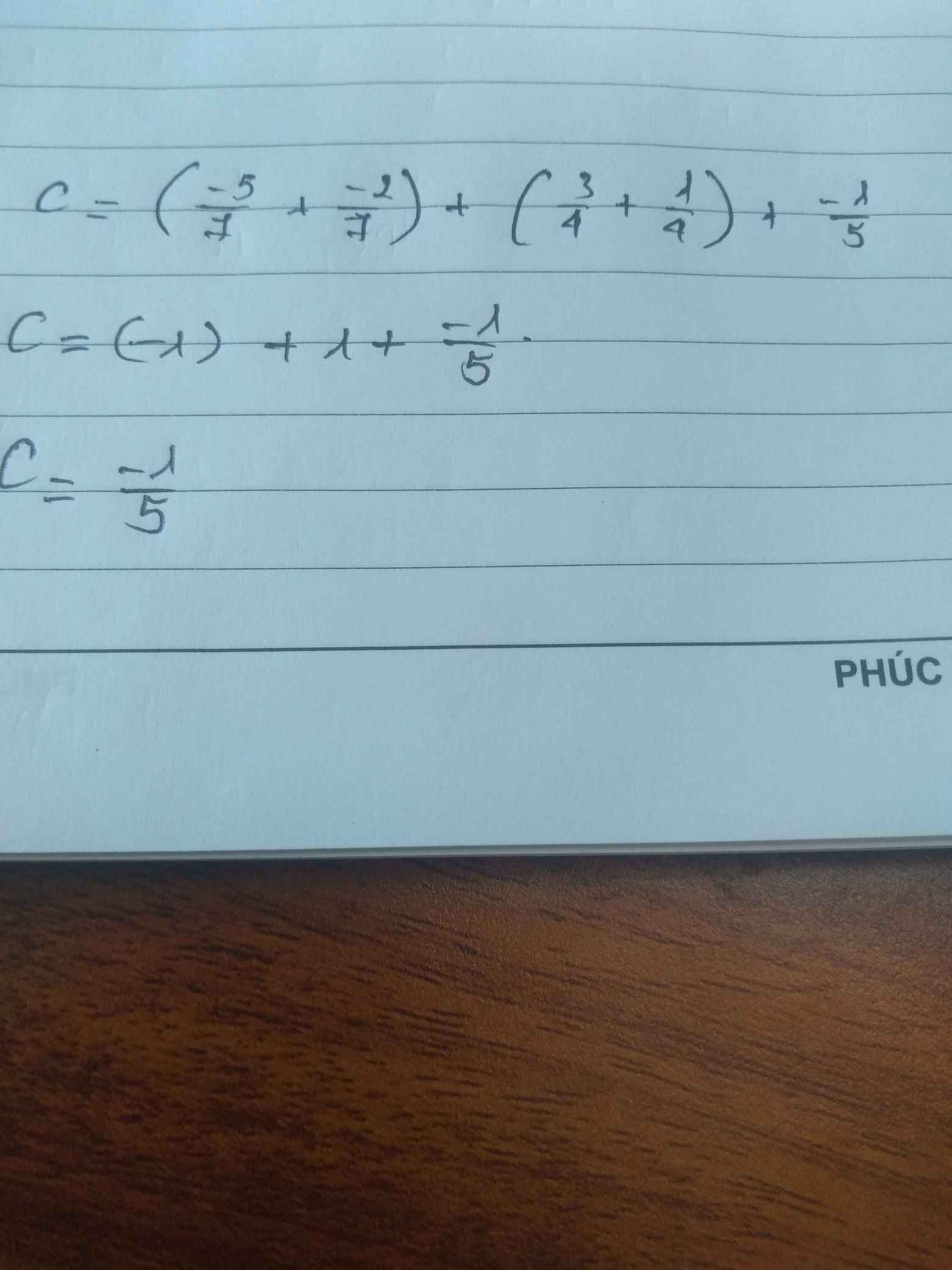
`@` `\text {Ans}`
`\downarrow`
\(\left(x-\dfrac{1}{5}\right)^2+1=3,5\div7\%\)
`=> (x-1/5)^2 + 1 = 3,5 \div 0,07`
`=> (x-1/5)^2 +1=50`
`=> (x-1/5)^2 = 49`
`=> (x-1/5)^2 = (+-7)^2`
`=>`\(\left[{}\begin{matrix}x-\dfrac{1}{5}=7\\x-\dfrac{1}{5}=-7\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=7+\dfrac{1}{5}\\x=-7+\dfrac{1}{5}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{36}{5}\\x=-\dfrac{34}{5}\end{matrix}\right.\)
Vậy, `x={36/5; -34/5}.`
Mình cảm ơn:3!