Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

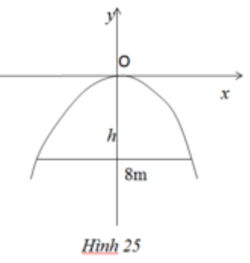
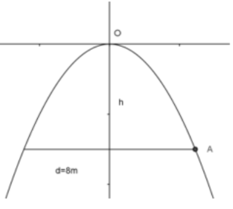
Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\left( {p > 0} \right)\)
Vì \(AB = 40cm\) và \(h = 30cm\) nên \(A\left( {30;20} \right)\)
Do \(A\left( {30;20} \right)\) thuộc parabol nên ta có: \({20^2} = 2p.30 \Rightarrow p = \frac{{20}}{3}\)
Vậy parabol có phương trình chính tắc là: \({y^2} = \frac{{40}}{3}x\)

Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)

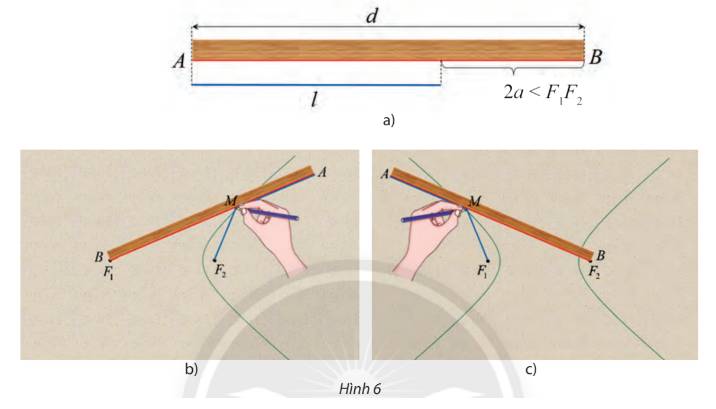
a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)

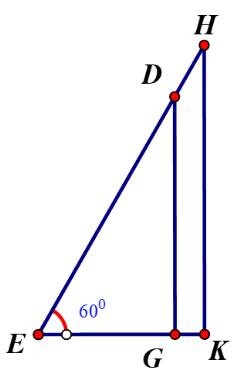
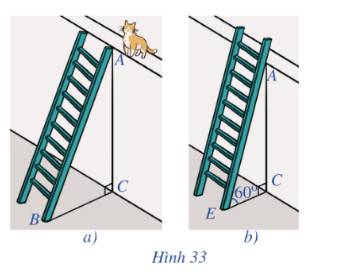
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.