Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

Bài 1: Ta có
\(y'=0\Leftrightarrow x[2mx^2-(m+1)]=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ 2mx^2-(m+1)=0(1)\end{matrix}\right.\)
Một điểm nằm trên trục tọa độ thì tung độ hoặc hoành độ phải bằng $0$. Do đó yêu cầu đề bài được đáp ứng khi $y'=0$ có nghiệm $x=0$ hoặc nếu $x$ khác $0$ thì tung độ tương ứng phải bằng $0$
+) Nếu \(m=0\) : $(1)$ vô nghiệm . $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu $m=-1$ : $(1)$ có nghiệm $x=0$ (thỏa mãn)
+) Nếu $-1< m< 0$. Từ \((1)\Rightarrow x^2=\frac{m+1}{2m}< 0\) (vô lý) nên $(1)$ vô nghiệm. $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu \(m>0\) hoặc \(m< -1\)
$(1)$ có 2 nghiệm \(x=\pm \sqrt{\frac{m+1}{2m}}\neq 0\)
\(\Rightarrow y=m(\pm \sqrt{\frac{m+1}{2m}})^4-(m+1)(\pm \sqrt{\frac{m+1}{2m}})^2+(m+1)\)
\(=\frac{(m+1)^2}{4m}-\frac{(m+1)^2}{2m}+(m+1)\)
\(=(m+1)-\frac{(m+1)^2}{4m}=0\)
\(\Leftrightarrow \left[\begin{matrix} m=-1\\ m=\frac{1}{3}\end{matrix}\right.\) . Vì \(\Rightarrow m=\frac{1}{3}\)
Vậy \(-1\leq m\leq 1 \text{or m}=\frac{1}{3}\)
Bài 2:
Ta có: \(y'=4x^3+4mx=0\Leftrightarrow x(x^2+m)=0\)
Nếu $m\geq 0$. PT $y'=0$ có duy nhất nghiệm $x=0$. Ta chỉ thu được 1 điểm cực trị (loại)
Nếu $m<0$. Ngoài $x=0$ pt $y'=0$ còn có 2 nghiệm \(x=\pm \sqrt{-m}\neq 0\)
(thu được 3 cực trị)
Khi đó:
\(y=(\pm \sqrt{-m})^4+2m(\pm \sqrt{-m})^2+4=m^2-2m^2+4=4-m^2\)
Để điểm cực trị nằm trên trục tọa độ thì \(y=0\Leftrightarrow 4-m^2=0\Leftrightarrow m=-2\) (do $m< 0$)
Vậy \(m=-2\)

+ Phương trình hoành độ giao điểm của đồ thị C và trục Ox:
x3- 3( m+ 1) x2+ 2( m 2+ 4m+1 )= 0
hay ( x- 2) ( x2-( 3m+ 1) x+ 2m2+ 2m) =0
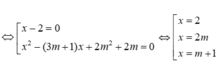
Yêu cầu bài toán
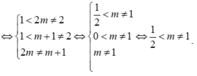
Vậy ½< m và m≠ 1.
Chọn A.
Phương trình hoành độ giao điểm của đồ thị (C) và trục Ox:
x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1)=0
hay (x-2) (x2-(3m+1) x+2m2+2m)=0
Chọn A.