Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
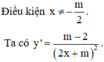
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364

Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Chọn B
Phương pháp: Sử dụng đạo hàm của hàm hợp để tính đạo hàm.


Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.





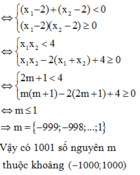
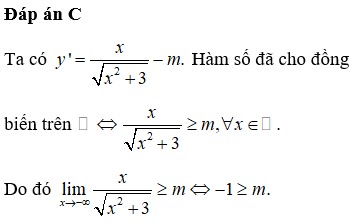

Đáp án D
Hàm số đồng biến trên khoảng (2;+∞)
⇔ y’ ≥ 0 ∀ x ϵ D (2;+∞)
Ta có: (-m; +∞) = D (2;+∞)
ð m ≥ -2
Ta có: y’ = m 2 − 3 ( x + m ) 2
ð y’ ≥ 0 ⇔ m ≥ 3 hoặc m ≤ - 3
Vậy tập giá trị m thỏa mãn đề bài là: m ≥ 3 hoặc -2 ≤ m ≤ - 3