Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi pt d có dạng \(y=ax+b\)
\(f\left(x\right)-g\left(x\right)\le0\Leftrightarrow x^2-ax-b\le0\)
Do nghiệm của BPT là \(\left[1;3\right]\Rightarrow f\left(x\right)-g\left(x\right)=0\) có 2 nghiệm pb \(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Theo Viet đảo: \(\left\{{}\begin{matrix}a=3+1\\-b=3.1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=-3\end{matrix}\right.\) \(\Rightarrow y=4x-3\Leftrightarrow4x-y-3=0\)
\(\Rightarrow A\left(1;1\right)\) ; \(B\left(3;9\right)\)
Diện tích tam giác ABM lớn nhất khi \(d\left(M;d\right)\) lớn nhất
\(d\left(M;d\right)=\frac{\left|4m-m^2-3\right|}{\sqrt{17}}=\frac{\left|m^2-4m+3\right|}{\sqrt{17}}=\frac{\left|\left(m-2\right)^2-1\right|}{\sqrt{17}}\le\frac{1}{\sqrt{17}}\)
Dấu "=" xảy ra khi \(m=2\)

gọi vtpt \(\Delta_1\)là \(\overrightarrow{n_1}\)=(m;1)
vtpt\(\Delta_2\) là \(\overrightarrow{n_2}\)=(1;-1)
để hai đường thẳng vuông góc thì \(\overrightarrow{n_1}\)\(\times\)\(\overrightarrow{n_2}\)=\(\overrightarrow{0}\)<=>m\(\times\)1-1=0<=> m=1

Câu 2: (d) : y= kx + x+ 2
Vì (d) cắt trục hoành tại điểm có hoành độ bằng 1
nên (d) sẽ cắt A(1;0)
A(1;0) ∈ (d) ⇔ 0 = k +1+2 ⇔ k= -3
Vậy k = -3
Câu 3:
y = f(x) = \(x^2-4x+3\)
TXĐ: D = R
Đỉnh I (2;-1)
Vì a > 0 nên hàm số đồng biến trên khoảng (-∞ ; 2) và nghịch biến trên khoảng (2;+∞)
Ta có: hàm số nằm trên đoạn [ -2;1]
Suy ra: giá trị lớn nhất đạt được khi x= -2 và giá trị nhỏ nhất đạt được khi x = 1
Với x = -2 ⇒ y = 15
Với x = 1 ⇒ y= 0
Vậy giá trị lớn nhất M = 15 , giá trị nhỏ nhất m = 0

Bài 1: Vì đường thẳng y=3 cắt đồ thị hàm số \(y=ax^2+bx+c\) tại hai điểm có hoành độ là -1 và 3 nên ta có: \(\left\{{}\begin{matrix}a.\left(-1\right)^2+b.\left(-1\right)+c=3\\a.3^2+b.3+c=3\end{matrix}\right.\)(1)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b+c=3\\9a+3b+c=3\end{matrix}\right.\)
lại có hàm số đạt GTNN bằng -1 nên ta có: \(\dfrac{-\Delta}{4a}=-1\Leftrightarrow b^2-4ac=4a\)(2)
Từ (1) (2) ta có hệ pt: \(\left\{{}\begin{matrix}a-b+c=3\\9a+3b+c=3\\b^2=4ac+4a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a+4b=0\\a-b+c=3\\b^2=4ac+4a\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\a-b+c=3\\b^2+2bc+2b=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\a-b+c=3\\b\left(b+2c+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\a-b+c=3\\b=0\end{matrix}\right.\)hoặc\(\left\{{}\begin{matrix}b=-2a\\a-b+c=3\\b+2c=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=0\\c=3\end{matrix}\right.\)(vô lý) hoặc \(\left\{{}\begin{matrix}a=-\dfrac{b}{2}\\-\dfrac{3}{2}b+c=3\\\dfrac{1}{2}b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=0\end{matrix}\right.\)
Bài 2: Hoành độ giao điểm của (P) và (d) là nghiệm của pt:
\(-x^2+4x-2=-2x+3m\)\(\Leftrightarrow x^2-6x+3m+2=0\)
\(\Rightarrow\Delta'=\left(-3\right)^2-3m-2=7-3m\)
Để pt có nghiệm thì \(\Delta'\ge0\Leftrightarrow7-3m\ge0\Leftrightarrow\dfrac{7}{3}\ge m\)
Để (d) và (P) có giao điểm nằm trên đt y=-2 thì tồn tại giá trị x và m là nghiệm của hệ pt: \(\left\{{}\begin{matrix}-x^2+4x-2=-2\\-2x+3m=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x^2-4x=0\\2x-3m=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\m=-\dfrac{2}{3}\end{matrix}\right.\)(thỏa mãn) hoặc \(\left\{{}\begin{matrix}x=4\\m=2\end{matrix}\right.\)(thỏa mãn)

\(\left\{{}\begin{matrix}mx+y=0\\-x+my=\sqrt{m^2+1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2x+my=0\\-x+my=\sqrt{m^2+1}\end{matrix}\right.\) \(\Rightarrow\left(m^2+1\right)x=-\sqrt{m^2+1}\Rightarrow x=\frac{-1}{\sqrt{m^2+1}}\)
\(\Rightarrow y=-mx=\frac{m}{\sqrt{m^2+1}}\)
Ta có \(x^2+y^2=\frac{1}{m^2+1}+\frac{m^2}{m^2+1}=1\)
\(\Rightarrow\) Quỹ tích giao điểm là nửa bên trái đường tròn \(x^2+y^2=1\) (do \(x< 0\) nên chỉ có 1 nửa đường tròn)

Pt hoành độ giao điểm: \(x^2-2mx+m=2x-1\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+m+1=0\)
\(\Delta'=\left(m+1\right)^2-\left(m+1\right)>0\Leftrightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\) (1)
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2\le12\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\le12\)
\(\Leftrightarrow4\left(m+1\right)^2-2\left(m+1\right)-12\le0\)
\(\Leftrightarrow2m^2+3m-5\le0\Rightarrow-\frac{5}{2}\le m\le1\) (2)
Kết hợp (1); (2) \(\Rightarrow\left[{}\begin{matrix}-\frac{5}{2}\le m< -1\\0< m\le1\end{matrix}\right.\)
+ đường thẳng ∆1 có VTCP
+ đường thẳng ∆2 có VTCP
Để hai đường thẳng vuông góc thì
Nên: -3( m2+ 1) +(-m) .(-4m) = 0 =>m2-3= 0=>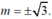
Chọn A.