
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


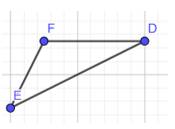
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
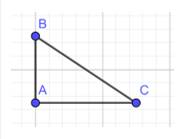
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A

a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.

b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác

Gọi cạnh còn lại có độ dài là \(x\), theo bất đẳng thức tam giác ta có:
\(7-1< x< 7+1\Rightarrow6< x< 8\)
⇒ \(x=7\)
Chọn D
Gọi độ dài cạnh còn lại của tam giác là `x (x \ne 0,`\(\in N\)\(\text{*}\) `)`
Theo bất đẳng thức tam giác ta có:
`1+7 > x > 7-1`
`-> 8> x> 6`
`-> x= {7}`
Xét các đáp án `-> D (tm)`

Gọi độ dài cạnh thứ ba của tam giác là x cm (x > 0)
Áp dụng bất đẳng thức trong tam giác ta có: 10 – 2 < x < 10 + 2
Hay 8 < x < 12
Trong bốn đáp án A, B, C, D thì đáp án D thỏa mãn vì 8 < 9 < 12
Vậy độ dài cạnh thứ ba là 9 cm.
Chọn đáp án D

a) Có, vì 12 < 5 + 10.
b) Không, vì 1 + 2 = 3
c) Có, vì 9 < 6 + 8.
với giá trị nào của a thì a, 6, 10 là độ dài ba cạnh của 1 tam giác
Trả lời :
a =8
~sai xl~
a < 16 (theo định lý)
k giúp mình
làm ơn