Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hai đường trùng nhau thì k-2=6-2k và -2m+5=m-1
=>3k=8 và -3m=-6
=>k=8/3 và m=2
b: Để hai đường song song thì k-2=6-2k và -2m+5<>m-1
=>k=8/3 và m<>2
c: Để hai đường cắt nhau thì k-2<>6-2k
=>k<>8/3
d: Để hai đường cắt nhau trên trục tung thì k-2<>6-2k và -2m+5=m-1
=>m=2 và k<>8/3
e: m=3
=>(d1): y=(k-2)x+2 và (d2): y=(6-2k)x-1
Để hai đường cắt nhau trên trục hoành thì k-2<>6-2k và -2/k-2=1/6-2k
=>k<>8/3 và -12+4k=k-2
=>3k=10 và k<>8/3
=>k=10/3

Lời giải:
Để hai đường thẳng song song nhau thì:
\(\left\{\begin{matrix} k+3=4\\ m+1\neq 3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m\neq 1\end{matrix}\right.\)
Để hai đt cắt nhau thì: \(\left\{\begin{matrix} k+3\neq 4\\ m\in\mathbb{R}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k\neq 1\\ m\in\mathbb{R}\end{matrix}\right.\)
Để hai đt trùng nhau thì: \(\left\{\begin{matrix} k+3=4\\ m+1=3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m=1\end{matrix}\right.\)
Để hai đt cắt nhau tại 1 điểm trên trục tung thì:
PT hoành độ giao điểm $(k+3)x+m+1=4x+3-m$ nhận $x=0$ là nghiệm
$\Leftrightarrow x(k-1)+(2m-2)=0$ nhận $x=0$ là nghiệm
$\Leftrightarrow 2m-2=0$
$\Leftrightarrow m=1$
Vậy $m=1$ và $k\in\mathbb{R}$ bất kỳ.
Để 2 đt vuông góc thì $(k+3).4=-1$ và $m$ bất kỳ
$\Leftrightarrow k=\frac{-13}{4}$ và $m$ bất kỳ.

Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
HT

Hàm số y = 2x + 3k có các hệ số a = 2, b = 3k.
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a' = 2m + 1, b' = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
![]()
a) Hai đường thẳng cắt nhau khi a ≠ a' tức là:
2 ≠ 2m + 1 ⇔ 2m ≠ 1

b) Hai đường thẳng song song với nhau khi a = a' và b ≠ b' tức là:
2 = 2m + 1 và 3k ≠ 2k – 3

c) Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
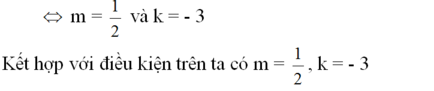

a, cắt : a khác a'
b, b= b'; a khác a'
c, a=a' ; b khác b'
d, a*a'= -1
e, a= a' ;b= b'

a) Hai đường thẳng cắt nhau khi 2m + 1 ≠ 2 hay m ≠ 0,5, k túy ý.
b) Hai đường thẳng song song với nhau khi 2m + 1 = 2 và 3k ≠ 2k - 3 hay khi m = 0,5 và k ≠ -3.
c) Hai đường thẳng trùng nhau khi 2m + 1 = 2 và 3k = 2k - 3 hay khi m = 0,5 và k = -3.
Bài giải:
a) Hai đường thẳng cắt nhau khi 2m + 1 ≠ 2 hay m ≠ 0,5, k túy ý.
b) Hai đường thẳng song song với nhau khi 2m + 1 = 2 và 3k ≠ 2k - 3 hay khi m = 0,5 và k ≠ -3.
c) Hai đường thẳng trùng nhau khi 2m + 1 = 2 và 3k = 2k - 3 hay khi m = 0,5 và k = -3

a) Hàm số \(y=2x+3k\) có các hệ số \(a=2,b=3k\)
Hàm số \(y=\left(2m+1\right)x+2k-3\) có các hệ số \(a'=2m+1,b'=2k-3\)
Hai hàm số đã cho là hàm số bậc nhất nên \(2m+1\ne0\)
\(\Leftrightarrow m\ne-\frac{1}{2}\)
Hai đường thẳng song song với nhau khi \(a=a'\) và \(b\ne b'\) tức là:
\(2=2m+1\) và \(3k\ne2k-3\)
Kết hợp với điều kiện trên ta có: \(m=\frac{1}{2}.k\ne-3\)
b) Hai đường thẳng song song:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k\ne2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k\ne-3\end{cases}}\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k=2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k=-3\end{cases}}\)
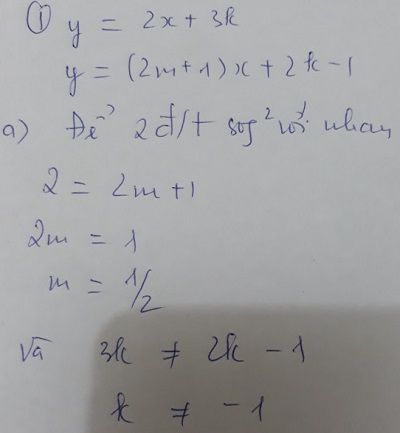 câu a đây mong bạn tham thảo
câu a đây mong bạn tham thảo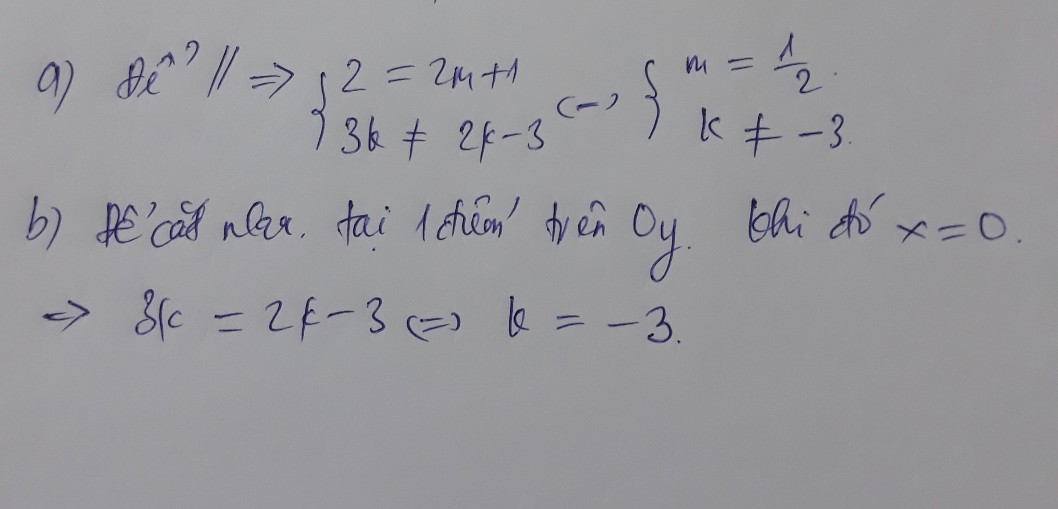
a) Trùng nhau :\(\Leftrightarrow\hept{\begin{cases}k-2=6-2k\\m-1=5-2m\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}k=\frac{8}{3}\\m=2\end{cases}}\)
b) Song song \(\Leftrightarrow\hept{\begin{cases}k-2=6-2k\\m-1\ne5-2m\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}k=\frac{8}{3}\\m\ne2\end{cases}}\)
c) Cắt nhau\(\Leftrightarrow k-2\ne6-2k\)\(\Leftrightarrow k\ne\frac{8}{3}\)
d) Vuông góc với nhau \(\Leftrightarrow\left(k-2\right).\left(6-2k\right)=-1\)
\(\Leftrightarrow-2k^2+10k-12=-1\)
\(\Leftrightarrow2k^2-10k+12=1\)
\(\Leftrightarrow2k^2-10k+11=0\)
\(\Leftrightarrow\orbr{\begin{cases}k=\frac{5+\sqrt{3}}{2}\\k=\frac{5-\sqrt{3}}{2}\end{cases}}\)