Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Trước tiên ta đếm số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho.
Gọi số có 4 chữ số là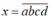 
Có 5 cách chọn a(vì a khác 0); khi đó có 
cách chọn bcd từ 5 số còn lại.
Theo quy tắc nhân có: 
số.
+ Tiếp theo, số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho mà không có mặt chữ số 1
Gọi số có 4 chữ số là
Có 4 cách chọn a(vì a khác 0); khi đó có 
cách chọn bcd từ 4 số còn lại.
Theo quy tắc nhân có 
số
Vậy số các số tự nhiên có bốn chữ số khác nhau mà nhất thiết phải có mặt số 1 là:
300 – 96 = 204.
Chọn A.
Đáp án B
Số đó nhất thiết phải có mặt 3 chữ số 1, 2, 5 ta chỉ cần chọn 2 chữ số nữa từ 4 chữ số còn lại.
TH1: Hai chữ số được chọn kia không chứa số 0: Ta có 
TH2: Hai chữ số kia chứa chữ số 0, ta loại trường hợp chữ số 0 đứng đầu thì còn: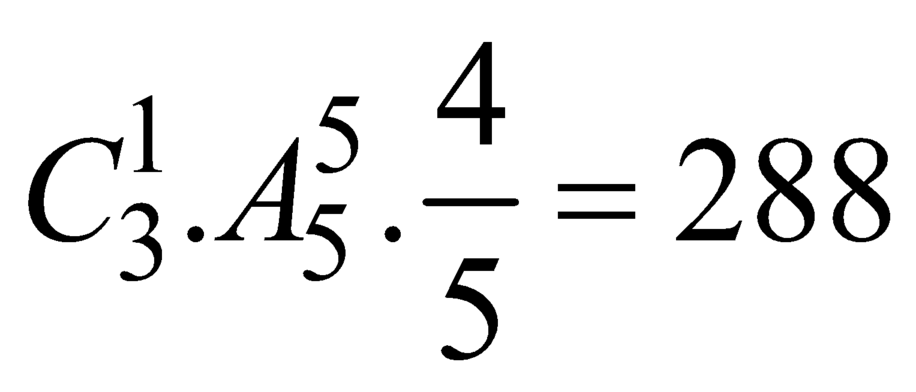 
Vậy có tất cả là 648 số
Gọi số cần lập 
Bước 1: Xếp chữ số 0 vào 1 trong 5 vị trí từ a2 đến a6, có 5 cách xếp.
Bước 2: Xếp chữ số 1 vào 1 trong 5 vị trí còn lại (bỏ 1 vị trí chữ số 0 đã chọn), có 5 cách xếp.
Bước 3: Chọn 4 chữ số trong 8 chữ số {2, 3, 4, 5, 6 , 7, 8, 9}để xếp vào 4 vị trí còn lại, có 
cách.
Theo quy tắc nhân có 
số thỏa yêu cầu.
Chọn D.
a. Gọi chữ số cần lập là \(\overline{abcd}\)
TH1: \(d=0\Rightarrow\) bộ abc có \(A_9^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 4 cách chọn (từ 2,4,6,8)
a có 8 cách chọn (khác 0 và d), b có 8 cách chọn (khác a và d), c có 7 cách chọn (khác a,b,d)
\(\Rightarrow4.8.8.7\) số
Tổng cộng: \(A_9^3+4.8.8.7=...\)
b. Chọn 4 chữ số còn lại: có \(C_7^4\) cách
Hoán vị 3 chữ số 0,1,2: có \(3!\) cách
Coi bộ 3 chữ số này là 1 số, hoán vị với 4 chữ số còn lại: \(5!\) cách
Ta đi tính số trường hợp 0 đứng đầu:
Số 0 đứng đầu trong bộ 0,1,2: có \(2!\) cách
Đặt bộ 0,1,2 đứng đầu, xếp vị trí cho 4 chữ số còn lại: \(4!\) cách
Vậy có: \(C_7^4.\left(3!.5!-2!.4!\right)=...\) số
Chọn 5 chữ số từ 9 chữ số còn lại và hoán vị chúng: \(A_9^5\) cách
5 chữ số đã cho tạo thành 6 khe trống, xếp 3 chữ số 1 vào 6 khe trống đó: \(C_6^3\) cách
\(\Rightarrow A_9^5.C_6^3\) số (bao gồm cả trường hợp số 0 đứng đầu)
Chọn 5 chữ số, trong đó có mặt chữ số 0: \(C_8^4\) cách
Xếp 5 chữ số sao cho số 0 đứng đầu: \(4!\) cách
5 chữ số (trong đó vị trí 0 đứng đầu cố định) tạo ra 5 khe trống, xếp 3 chữ số 1 vào 5 khe trống đó: \(C_5^3\) cách
\(\Rightarrow\) Tổng cộng có: \(A_9^5.C_6^3-C_8^4.4!.C_5^3\) số thỏa mãn
TH1: số 2 đứng đầu:
Chọn 2 chữ số từ 6 chữ số còn lại và hoán vị: \(A_6^2=30\) cách
TH2: số 2 không đứng đầu:
Chọn số hàng trăm: có 5 cách (khác 0 và 2)
Chọn 1 chữ số còn lại: 5 cách, hoán vị nó với 2: có \(2!=2\) cách
\(\Rightarrow5.5.2=50\) cách
Tổng cộng: \(30+50=80\) số
+ Nếu số hàng nghìn khác 0 thì số các số có 4 chữ số khác nhau là : 5 . 5 . 4 . 3 . 2 = 600 số
+ Nếu không có mặt chữ số 1 thì số các số cho 4 chữ số khau nhau là
4 . 4 . 3 . 2 = 96 số
+ Nếu không có mặt chữ số 2 thì số các số có 4 chữ số khau nhau là
4 . 4 . 3 . 2 = 96 số
Vậy nếu không có mặt chữ số 1 hoặc 2 thì sẽ có 96 . 2 = 192 số
Vậy nếu phải xuất hiện cả số 1 và 2 thì số các số có 4 chữ số khác nhau là 600 - 192 = 408 (số)