K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2023
a \(\dfrac{1}{x-y}+\dfrac{2}{x+y}+\dfrac{3x}{y^2-x^2}\)
\(=\dfrac{x+y+2x-2y-3x}{\left(x-y\right)\left(x+y\right)}=\dfrac{-y}{\left(x-y\right)\left(x+y\right)}\)
b: \(\dfrac{1}{x-2}+\dfrac{1}{x+2}-\dfrac{4x-4}{x^2-4}\)
\(=\dfrac{x+2+x-2-4x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{-2x+4}{\left(x-2\right)\left(x+2\right)}\)
=-2/x+2
c: \(\dfrac{x+1}{x+3}-\dfrac{x-1}{3-x}+\dfrac{2x-2x^2}{x^2-9}\)
\(=\dfrac{\left(x+1\right)\left(x-3\right)+\left(x-1\right)\left(x+3\right)+2x-2x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{2x-6}{\left(x+3\right)\left(x-3\right)}=\dfrac{2}{x+3}\)
CM
30 tháng 11 2017
ĐKXD: x ≠ {2, 3, 4, 5}
Phương trình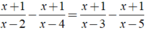
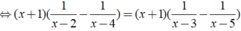
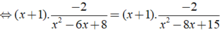
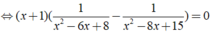
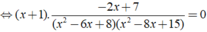
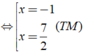
Vậy nghiệm của phương trình là x = - 1;x = 7/2
Chọn đáp án C.
7 tháng 8 2023
x^8+x^7+1
=x^8+x^7+x^6-x^6+1
=x^6(x^2+x+1)-(x^3-1)(x^3+1)
=x^6(x^2+x+1)-(x^3+1)(x-1)(x^2+x+1)
=(x^2+x+1)[x^6-(x^3+1)(x-1)]
=(x^2+x+1)(x^6-x^4+x^3-x+1]
b: x^8+x^4+1
=x^8+2x^4+1-x^4
=(x^4+1)^2-x^4
=(x^4+x^2+1)(x^4-x^2+1)
=(x^4-x^2+1)(x^4+2x^2+1-x^2)
=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)
c: x^5+x+1
=x^5-x^2+x^2+x+1
=x^2(x^3-1)+(x^2+x+1)
=x^2(x-1)(x^2+x+1)+(x^2+x+1)
=(x^2+x+1)(x^3-x^2+1)
d: x^3+x^2+4
=x^3+2x^2-x^2+4
=x^2(x+2)-(x-2)(x+2)
=(x+2)(x^2-x+2)
RG
0
