Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử đường tròn cần lập có tâm O; bán kính R.
Đường thẳng Δ đi qua M(2; -2) và có VTPT là n→(4; 3) nên đường thẳng này có 1 VTCP là u→(3; -4) . Phương trình tham số của đường thẳng Δ là:
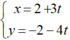
O nằm trên Δ ⇒ O(2 + 3t; -2 – 4t)
Đường tròn (O; R) tiếp xúc với d1 và d2 ⇒ d(O; d1) = d(O; d2) = R
Ta có: d(O; d1) = d(O; d2)
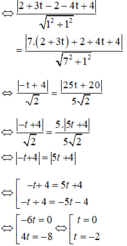
+ Với t = 0 ⇒ O(2; -2) ⇒ R = d(O; d1) = 2√2
Phương trình đường tròn: (x – 2)2 + (y + 2)2 = 8.
+ Với t = -2 ⇒ O(-4; 6) , R = d(O; d1) = 3√2
Phương trình đường tròn: (x + 4)2 + (y – 6)2 = 18
Vậy có hai phương trình đường tròn thỏa mãn là:
(x – 2)2 + (y + 2)2 = 8 hoặc (x + 4)2 + (y – 6)2 = 18
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
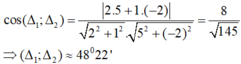
Chọn C.
Ta có:
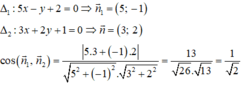
Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 ° .
Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
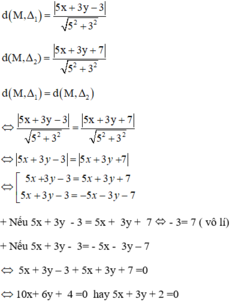
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là đường thẳng: 5x + 3y + 2 = 0.
Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)
Cách 1:
Δ1: y = –2x + 4 ⇔ 2x + y – 4 = 0
Δ2: 
⇔ x - 2y + 3 = 0
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(1;-2)
Góc giữa (Δ1) và (Δ2):
Cách 2:
Δ1: y = –2x + 4 có hệ số góc k1 = –2
Δ2: 
có hệ số góc k2 = 1/2
Nhận thấy k1.k2 = –1 nên Δ1 ⊥ Δ2 ⇒ (Δ1, Δ2) = 90°.
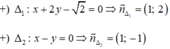
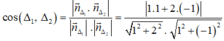
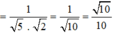
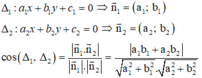
Vì (C) tiếp xúc với hai đường thẳng đã cho nên tâm của (C) nằm trên đường phân giác của góc tạo bởi hai đường thẳng đó
Phương trình đường phân giác:
\(\frac{\left|x+y+4\right|}{\sqrt{2}}=\frac{\left|7x-y+4\right|}{5\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}5\left(x+y+4\right)=7x-y+4\\5\left(x+y+4\right)=-7x+y-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x+6y+16=0\\12x+4y+24=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-3y-8=0\\3x+y+6=0\end{matrix}\right.\)
TH1: Nếu phương trình đường phân giác là x-3y-8=0. Khi đó tâm của (C) là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-3y-8=0\\4x+3y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)
Phương trình đường tròn (C) là: (x-2)2+(y+2)2=\(\left(\frac{\left|2-2+4\right|}{\sqrt{2}}\right)^2=8\)
TH2:Nếu phương trình đường phân giác là 3x+y+6=0. Phương trình đường tròn là:
(x+4)2+(y-6)2=18