Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{x^2+xy+y^2}{x-y}=\frac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x-y\right)^2}=\frac{x^3-y^3}{\left(x-y\right)^2}\)
\(\frac{x^2+xy+y^2}{x-y}\)
\(=\frac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x-y\right)^2}\)
\(=\frac{x^3-y^3}{x^2-2xy+y^2}\)

Thông báo thay trang thay mặt người phân phối chương trình xin tặng chương trình học online số 1 Việt Nam. Sự kiện bắt đầu từ ngày 28/10 đến 1/11
Xin chào các thành viên đang online trên trang. Sự kiện khuyến mãi được tài trợ 500 suất áo chiếc áo đá bóng Việt Nam.Mong tất cả mọi người đã xem vào truy cập sau để nhận thưởng khi xem có 1 bản đăng kí nhận miễn phí : Thời gian có hạn tặng mọi người đã tham gia tích cực -> Không tin các bạn có thể hỏi các CTV nha mình chỉ có quyền thông báo :
Copy cái này hoặc gõ :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
--

a)Ta có:
3x2−4x−17x+2=3x−10+3x+23x2−4x−17x+2=3x−10+3x+2
Để phân thức là số nguyên thì 3x+23x+2 phải là số nguyên (với giá trị nguyên của x).
3x+23x+2 nguyên thì x +2 phải là ước của 3.
Các ước của 3 là ±1,±3±1,±3 . Do đó
x+2=±1=>x=−1,x=−3x+2=±1=>x=−1,x=−3
x+2=±3=>x=1,x=−5x+2=±3=>x=1,x=−5
Vậy x=−5;−3;

a/ \(\left(x+\dfrac{4}{3}y^2\right)^2\)
\(=x^2+2.x.\dfrac{4}{3}y^2+\left(\dfrac{4}{3}y^2\right)^2\)
\(=x^2+\dfrac{8}{3}xy^2+\dfrac{16}{9}y^4\)
b/ \(\left(2x^2+\dfrac{5}{3}y\right)^2\)
\(=\left(2x^2\right)^2+2.2x^2.\dfrac{5}{3}y+\left(\dfrac{5}{3}y\right)^2\)
\(=4x^4+\dfrac{20}{3}x^2y+\dfrac{25}{9}y^2\)

a, \(\left(x-y+z\right)\left(x-y-z\right)\)
\(=\left(x-y\right)^2-z^2\)(hằng đẳng thức số 3)
b, Sửa đề:\(\left(\dfrac{1}{2}x+y-z\right)\left(\dfrac{1}{2}x+y+z\right)\)
\(=\left(\dfrac{1}{2}x+y\right)^2-z^2\)(hằng đẳng thức số 3)
Chúc bạn học tốt!!!

Bài 1:
a) -16 +(x-3)2
<=> (x-3)2-16
<=> (x-3)2 -42
<=> (x-3-4)(x-3+4)
<=> (x-7)(x+1)
b) 64+16y+y2
<=> y2 + 2.8.y + 82
<=> (y+8)2
c) \(\dfrac{1}{8}-8x^3\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^3-\left(2x\right)^3\)
\(\Leftrightarrow\left(\dfrac{1}{2}-2x\right)\left(\dfrac{1}{4}+x+4x^2\right)\)
d)\(x^2-x+\dfrac{1}{4}\)
\(\Leftrightarrow x^2-2.\dfrac{1}{2}.x+\left(\dfrac{1}{2}\right)^2\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2\)
e) x4 + 4x2 + 4
<=> (x2)2 + 2.2.x2 +22
<=> (x2 + 2)2
g)\(8x^3+60x^2y+150xy^2+125y^3\)
\(\Leftrightarrow\left(2x+5y\right)^3\)

Ta có \(\frac{2}{x^3-y^3}=\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x-1}{x^2-y^2}=\frac{2x+1}{\left(x+y\right)\left(x-y\right)}\)
\(\frac{1}{x+y}\) giữ nguyên
MTC: \(\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)\)
Các nhân tử phụ tương ứng là : \(\left(x+y\right);\left(x-y\right)\left(x^2+xy+y^2\right);\left(x^2+xy+y^2\right)\)
Ta có:
\(\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\frac{2.\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{1}{x+y}=\frac{1.\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x+1}{\left(x+y\right)\left(x-y\right)}=\frac{\left(2x+1\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)

Bài giải
a) \(\dfrac{1}{x+2}=\dfrac{x.\left(x-2\right)}{\left(x+2\right)\left(x-2\right).x}=\dfrac{x^2-2x}{x\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{8}{x\left(2-x\right)}=-\dfrac{8}{x\left(x-2\right)}=-\dfrac{8.\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
b) \(x^2+1=\dfrac{x^2+1}{1}=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}\) giữ nguyên.
c) \(\dfrac{x^3}{x^3-3x^2y+3xy^2-y^3}=\dfrac{x^3}{\left(x-y\right)^3}=\dfrac{x^3.y}{\left(x-y\right)^3.y}=\dfrac{x^3y}{y\left(x-y\right)^3}\)
\(\dfrac{x}{y^2-xy}=\dfrac{x}{y.\left(y-x\right)}=-\dfrac{x}{y.\left(x-y\right)}=-\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right).\left(x-y\right)^2}=\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right)^3}\)

\(27-x^3\)
\(=3^3-x^3\)
\(=\left(3-x\right)\left(9+3x+x^2\right)\)
\(8x^3+0,001\)
\(=\left(2x\right)^3+\left(\dfrac{1}{10}\right)^3\)
\(=\left(2x+\dfrac{1}{10}\right)\left(4x^2-2x\dfrac{1}{10}+\left(\dfrac{1}{10}\right)^2\right)\)
\(=2\left(x+\dfrac{1}{5}\right)\left(4x^2-\dfrac{1}{5}x+\dfrac{1}{100}\right)\)
\(\dfrac{x^3}{125}-\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{5}\right)^3-\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left[\left(\dfrac{x}{5}\right)^2+\dfrac{x}{5}.\dfrac{y}{3}+\left(\dfrac{y}{3}\right)^2\right]\)
\(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left(\dfrac{x^2}{25}+\dfrac{xy}{15}+\dfrac{y^2}{9}\right)\)
b )
Dấu = thứ 3 :
Sửa lại : \(2\left(x+\dfrac{1}{20}\right)\)

Bài giải:
a) 3x - 6y = 3 . x - 3 . 2y = 3(x - 2y)
b) 2525x2 + 5x3 + x2y = x2 (2525 + 5x + y)
c) 14x2y – 21xy2 + 28x2y2 = 7xy . 2x - 7xy . 3y + 7xy . 4xy = 7xy(2x - 3y + 4xy)
d) 2525x(y - 1) - 2525y(y - 1) = 2525(y - 1)(x - y)
e) 10x(x - y) - 8y(y - x) =10x(x - y) - 8y[-(x - y)]
= 10x(x - y) + 8y(x - y)
= 2(x - y)(5x + 4y)
a,\(3x-6y=3\left(x-2y\right)\)
b,\(x^2(\dfrac{2}{5}+5x+y)\)
c,\(7xy\left(2x-3y+4xy\right)\)
d,\(\dfrac{2}{5}x\left(y-1\right)-\dfrac{2}{5}y\left(y-1\right)\)
=\(\dfrac{2}{5}\left(y-1\right)\left(x-y\right)\)
e,\(10x\left(x-y\right)-8y\left(y-x\right)=10x\left(x-y\right)+8y\left(x-y\right)\)
\(2\left(x-y\right)\left(5x+4y\right)\)
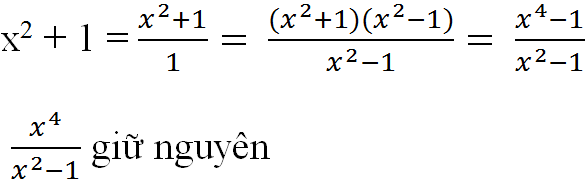
\(\dfrac{x-y}{x+y}\)=\(\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x^2+xy+y^2\right)}\)=\(\dfrac{x^3-y^3}{x^3+2x^2y+2xy^2+y^3}\)