
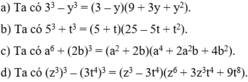
a) 27 –...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a/ \(\left(z^3\right)^3-\left(3t^4\right)^3=\left(z^3-3t^4\right)\left(z^6+3z^3t^4+9t^8\right)\) b/ \(\left(\frac{x}{2}\right)^3-\left(3y^2\right)^3=\left(\frac{x}{2}-3y^2\right)\left(\frac{x^2}{4}+\frac{3}{2}xy^2+9y^4\right)\) \(a,27-x^3\) \(=3^3-x^3\) \(=\left(3-x\right)\left(9+3x+x^2\right)\) Các câu còn lại lm tương tự nhé. hok tốt! a) \(27-x^3=\left(3-x\right)\left(9+3x+x^2\right)\) b) \(8x^3+0,001=\left(2x+0,1\right)\left(4x^2-0,2x+0,01\right)\) c) \(\frac{x^3}{125}-\frac{y^3}{27}=\left(\frac{x}{5}-\frac{y}{3}\right)\left(\frac{x^2}{25}+\frac{xy}{15}+\frac{y^2}{9}\right)\) p/s: chúc bạn học tốt \(27-x^3\) \(=3^3-x^3\) \(=\left(3-x\right)\left(9+3x+x^2\right)\) \(8x^3+0,001\) \(=\left(2x\right)^3+\left(\dfrac{1}{10}\right)^3\) \(=\left(2x+\dfrac{1}{10}\right)\left(4x^2-2x\dfrac{1}{10}+\left(\dfrac{1}{10}\right)^2\right)\) \(=2\left(x+\dfrac{1}{5}\right)\left(4x^2-\dfrac{1}{5}x+\dfrac{1}{100}\right)\) \(\dfrac{x^3}{125}-\dfrac{y^3}{27}\) \(=\left(\dfrac{x}{5}\right)^3-\left(\dfrac{y}{3}\right)^3\) \(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left[\left(\dfrac{x}{5}\right)^2+\dfrac{x}{5}.\dfrac{y}{3}+\left(\dfrac{y}{3}\right)^2\right]\) \(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left(\dfrac{x^2}{25}+\dfrac{xy}{15}+\dfrac{y^2}{9}\right)\) b ) Dấu = thứ 3 : Sửa lại : \(2\left(x+\dfrac{1}{20}\right)\) b) \(-4x^2-4x-1\) \(=-\left(4x^2+4x+1\right)\) \(=-\left(2x+1\right)^2\) c) \(\frac{4}{9}x^2-25y^2\) \(=\left(\frac{2}{3}x+5y\right)\left(\frac{2}{3}x-5y\right)\) d) \(\frac{1}{27}x^3-8\) \(=\left(\frac{1}{3}x-2\right)\left(\frac{1}{9}x+\frac{2}{3}x+4\right)\) Bài 1 : Viết các đa thức sau dưới dạng lập phương của một tổng hoặc lập phương của một hiệu a,8x3+12x2y+6xy2+y38x3+12x2y+6xy2+y3 = (2x)3 + 3.(2x)2.y + 3.2x.y2 + y3 = ( 2x + y )3 = x3 + 3.x2.1 + 3.x.12 + 13 =(x + 1)3 c, x3−3x2+2x−1x3−3x2+2x−1 = x3 - 3.x2.1+ 3.x.12 - 13 = (x - 1)3 d,27+27y2+9y4+y6 = 33 + 3.32.y2 + 3.3.y4 + (y2)3 = ( 3 + y2 ) 3 cho hỏi lập phương của 1 tổng hay 1 hiệu hay tổng hiệu 2 lập phương vậy bn viết đề vậy mk cx bí thui haizzzzzz a/ \(a^6+8b^3\) \(=\left(a^2\right)^3+2^3b^3\) \(=\left(a^2\right)^3+\left(2b\right)^3\) \(=\left(a^2+2b\right)\left(a^4-a^22b+4b^2\right)\) b/ \(z^9-27t^{12}\) \(=\left(z^3\right)^3-3^3\left(t^4\right)^3\) \(=\left(z^3\right)^3-\left(3t^4\right)^3\) \(=\left(z^3-3t^4\right)\left(z^6+z^33t^4+9t^8\right)\) a, \(x^3+8=x^3+2x^2-2x^2-4x+4x+8\) \(=x^2.\left(x+2\right)-2x.\left(x+2\right)+4.\left(x+2\right)\) \(=\left(x+2\right).\left(x^2-2x+4\right)\) \(\left(m-n\right)^6-6\left(m-n\right)^4+12\left(m-n\right)^2-8=\left[\left(m-n\right)^2-2\right]^3\) \(\dfrac{8}{27}a^3-\dfrac{8}{3}a^2b+8b^2a-8b^3=\left(\dfrac{2}{3}a-2b\right)^3\) Chúc bạn học tốt !!
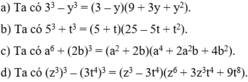





b,x3+3x2+3x+1x3+3x2+3x+1

