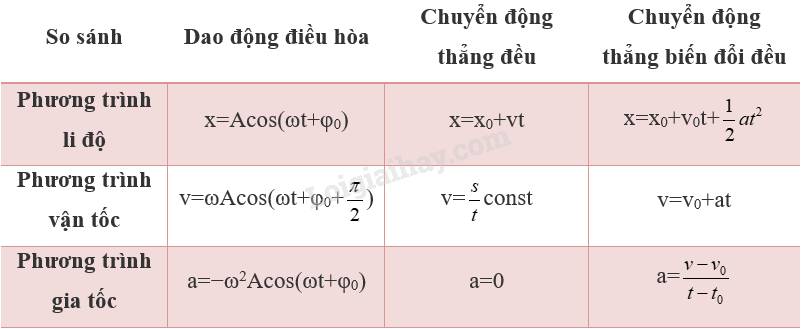
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

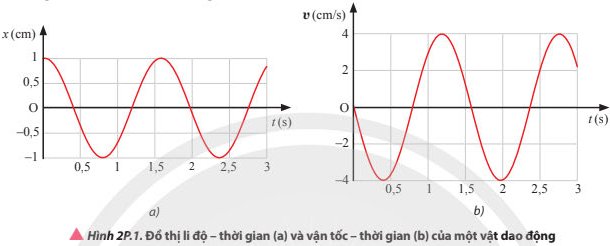
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)

Tốc độ cực đại của vật trong quá trình dao động là 0,4 m/s
Thế năng cực đại của vật trong quá trình dao động là
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.0,4^2=0,16\left(J\right)\).

2. Vật chuyển động tròn đều trên quĩ đạo thì có hình chiếu xuống một đường kính của quĩ đạo là dao động điều hòa. Do đó một dao động điều hòa có dạng
x = A cos(ωt+φ) có thể được biểu diễn tương đương với một chuyển động tròn đều nếu có:
- Tâm của đường tròn là VTCB 0
- Bán kính của đường tròn bằng với biên đọ dao động R = A
- Thời gian để chất điểm quay hết một vòng là một chu kì T
- Chiều quay của vật ngược chiều kim đồng hồ
- Góc mà bán kính nối vật chuyển động quét được trong quá trình vật chuyển động tròn đều Δφ = ωΔt

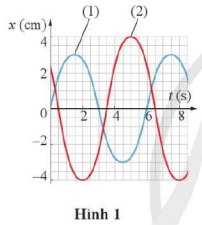
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)

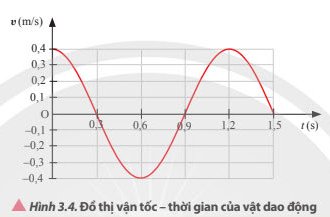
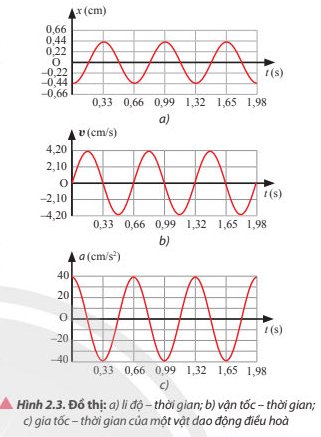
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)

tham khảo
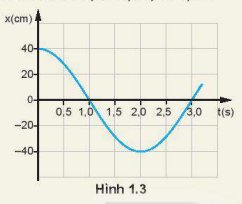
1. Mô tả dao động điều hòa của con lắc đơn:
+ Tại thời điểm ban đầu t = 0, con lắc đơn đang ở vị trí biên dương (x = A = 40 cm) và sẽ dịch chuyển về vị trí cân bằng, con lắc đơn ở vị trí x = 0 khi t = 1 s.
+ Tại thời điểm t = 1 s, con lắc đơn bắt đầu chuyển động về phía biên âm và ở vị trí x = - A = - 40 cm khi t = 2 s.
+ Tại thời điểm t = 2 s, con lắc đang ở vị trí biên âm sẽ dịch chuyển về vị trí cân bằng và ở tại vị trí x = 0 khi t = 3 s.
2. Sử dụng thước kẻ để xác định li độ của con lắc tại các thời điểm.
Cách làm: Từ các thời điểm bài toán yêu cầu, dựng đường thẳng vuông góc với trục thời gian tại vị trí thời điểm đó, đường thẳng cắt đồ thị tại điểm nào thì ta kẻ đường thẳng song song với trục thời gian đi qua điểm cắt đó. Đường thẳng song song này cắt trục Ox tại điểm nào thì đó là li độ cần tìm.
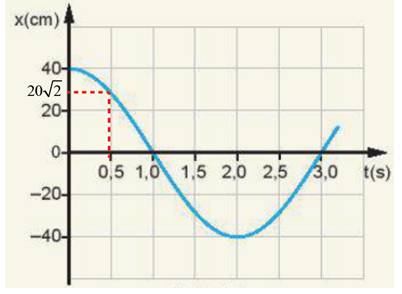
Tại thời điểm t = 0 vật bắt đầu xuất phát nên\(\left\{{}\begin{matrix}A=40cm\\x=40cm\end{matrix}\right.\)
Tại thời điểm t = 0,5 s: \(\left\{{}\begin{matrix}A=40cm\\x=20\sqrt{2}cm\end{matrix}\right.\)
Tại thời điểm t = 2,0 s, con lắc đang ở biên âm\(\left\{{}\begin{matrix}A=40cm\\x=-40cm\end{matrix}\right.\)

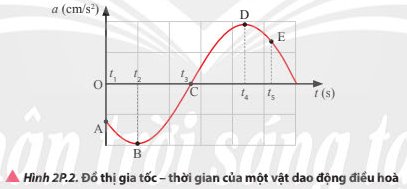
Vị trí A có gia tốc a1=−ω2.A
Vị trí B có gia tốc a2=0 nên vật ở vị trí cân bằng có vận tốc bằng v=ωA
Vị trí C có gia tốc a3=−ω2.A>0 nên vật ở vị trí biên âm có vận tốc bằng 0

a) Biên độ A= 2 mm
Tần số góc ω = 180π (rad/s)
Chu kì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{180\pi }} = \frac{1}{{90}}s\)
Tần số \(f = \frac{1}{T} = 90Hz\)
b) Phương trình vận tốc là:
v = −180π.2sin(180πt) = 360πsin(180πt) (mm/s)
Phương trình gia tốc là: a = −(180π)2.2cos(180πt) (mm/s2)