Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

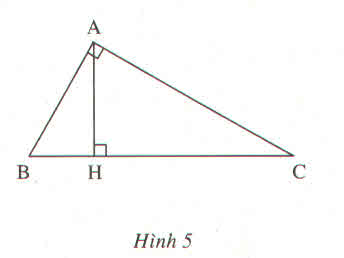
a,Trong \(\Delta\) ABH có AHB=900 (BH \(\perp\) BC tại H -gt)
AH2 + BH2 =AB2 (định lý Pi-ta-go)
T/s:162 +252 =AB2
\(\Rightarrow\) AB2 =881
mà AB>0
\(\Rightarrow\) AB=\(\sqrt{881}\)\(\approx\) 29.68
Trong\(\Delta\) ABC có BAC=900 (gt), Đường cao AH (gt)
AH2= BH*CH (hệ thức lượng)
T/s: 162=25*CH
\(\Rightarrow\) CH=\(\dfrac{16^2}{25}\) = 10.24
Có:BH+HC=BC(H\(\in\) BC)
T/s: 25+10.24=BC
\(\Rightarrow\) BC=35.24
Trong \(\Delta\) ABC có:BAC=900 (GT)
AB2 +AC2 =BC2(Định lý Py-ta-go)
T/s:29.682+AC2\(\approx\)35.242
\(\Rightarrow\) AC2\(\approx\)35.242-29.682
\(\approx\)360.95
Mà AC>0
\(\Rightarrow\) AC\(\approx\) 19

Áp dụng hệ thức lượng:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=4\left(cm\right)\)
\(BC=BH+CH=10\left(cm\right)\)
Hệ thức lượng:
\(AB^2=BH.BC\Rightarrow AB=\sqrt{BH.BC}=2\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{CH.BC}=4\sqrt[]{5}\) (cm)
\(sinB=\dfrac{AC}{BC}=\dfrac{2\sqrt{5}}{5}\)
\(cosB=\dfrac{AB}{BC}=\dfrac{\sqrt{5}}{5}\)
\(tanB=\dfrac{AC}{AB}=2\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=2+8=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=2\cdot8=16\)
hay AH=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=2\cdot10=20\\AC^2=8\cdot10=80\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{5}\left(cm\right)\\AC=4\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4\sqrt{5}}{10}=\dfrac{2\sqrt{5}}{5}\)
\(\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{2\sqrt{5}}{10}=\dfrac{\sqrt{5}}{5}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{4\sqrt{5}}{2\sqrt{5}}=2\)
\(\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{2\sqrt{5}}{4\sqrt{5}}=\dfrac{1}{2}\)

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)



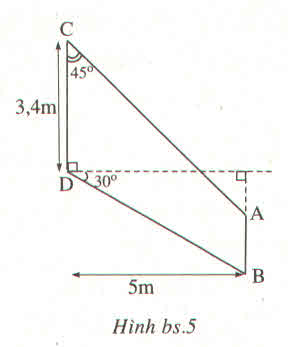





Xét ΔBCD vuông tại B có BH là đường cao ứng với cạnh huyền BD
nên \(\left\{{}\begin{matrix}BH^2=HC\cdot HD\\BC^2=CH\cdot CD\\BD^2=HD\cdot CD\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=4\left(cm\right)\\BC=2\sqrt{5}\left(cm\right)\\BD=4\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Gần đúng