Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ (cm)
$\sin B = \frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$
b.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$BE.BA=BH^2$
$AF.AC=AH^2$
$\Rightarrow BE.BA+AF.AC=BH^2+AH^2=AB^2$ (đpcm)

a: ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>AB^2=5^2-4^2=9
=>AB=3(cm)
ΔABC vuông tại A có sin B=AC/BC=4/5
nên \(\widehat{B}\simeq53^0\)
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2
=>BH=3^2/5=1,8cm
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC

A B H D E C I
a/
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH=\sqrt{HB.HC}=\sqrt{4.9}=6cm\)
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{6}{4}=\dfrac{3}{2}\)
b/
Xét tg vuông AHB có
\(HB^2=BD.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Xét tg vuông AHC có
\(HC^2=CE.AC\) (lý do như trên)
\(CE.BD.AC.AB=HB^2.HC^2=\left(HB.HC\right)^2\)
Mà \(HB.HC=AH^2\) (cmt)
\(\Rightarrow CE.BD.AC.AB=AH^4\)
c/
\(HD\perp AB;AC\perp AB\) => HD//AC => HD//AE
\(HE\perp AC;AB\perp AC\) => HE//AB => HE//AD
=> ADHE là hình bình hành mà \(\widehat{A}=90^o\) => ADHE là HCN
Xét tg vuông ADH và tg vuông ADE có
HD = AE (cạnh đối HCN)
AD chung
=> tg ADH = tg ADE (Hai tg vuông có 2 cạnh góc vuông = nhau)
\(\Rightarrow\widehat{AED}=\widehat{AHD}\)
\(\widehat{AHD}=\widehat{B}\) (cùng phụ với \(\widehat{BAH}\) )
\(\Rightarrow\widehat{AED}=\widehat{B}\) (1)
\(\widehat{C}+\widehat{B}=90^o\) (2)
\(\widehat{IAE}+\widehat{AED}=90^o\Rightarrow\widehat{IAE}+\widehat{B}=90^o\) (3)
Từ (2) và (3) => \(\widehat{IAE}=\widehat{C}\) => tg AIC cân tại I => IA=IC
Ta có
\(\widehat{IAE}+\widehat{BAI}=\widehat{A}=90^o\)
\(\Rightarrow\widehat{C}+\widehat{BAI}=90^o\) mà \(\widehat{C}+\widehat{B}=90^o\)
\(\Rightarrow\widehat{BAI}=\widehat{B}\) => tg ABI cân tại I => IA=IB
Mà IA= IC (cmt)
=> IB=IC => I là trung điểm của BC

Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
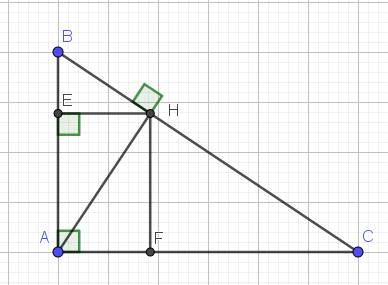
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)

b) Theo hệ thức lượng: AE.AB = AH2 ; AF.AC = AH2 => AE.AB = AF.AC.

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)
b: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
Do đó: ΔAEF đồng dạng với ΔACB
c: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)
ΔBAD vuông tại A có
\(cotABD=\dfrac{AB}{AD}\)(2)
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)

a) Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\)(Định lý Pytago)
\(\Rightarrow AC^2=BC^2-AB^2=10^2-6^2=64\Rightarrow AC=8\left(cm\right)\)
Xét tam giác ABC vuông tại A có đường cao AH
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{25}{576}\Rightarrow AH=\dfrac{24}{5}\left(cm\right)\)
Xét tứ giác AEHF có:
\(\widehat{AEH}=\widehat{EAF}=\widehat{AFH}=90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> \(EF=AH=\dfrac{24}{5}\left(cm\right)\)
b) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác ABH và tam giác AHC vuông tại H:
\(AH^2=AE.AB\)
\(AH^2=AF.AC\)
\(\Rightarrow AE.AB=AF.AC\)