PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
2
18 tháng 4 2017
Hướng dẫn vẽ:
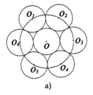
a) Trước hết vẽ đường tròn bán kính 1.2 cm rồi vẽ đường kình của đường tròn. Trên hai nửa mặt phẳng bờ đối nhau là đường kính vẽ hai nửa đường tròn có đường kính lần lượt là đoạn nối tâm tới một đầu của đường kính vừa vẽ. Sau cùng tô màu như hình vẽ.
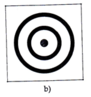
b) Trước hết, vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
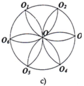
c) Trước hết vẽ đường tròn ở chính giữa có bán kình R. Vẽ một đường tròn phụ trùng với tâm đường tròn vừa vẽ, bán kính 2 R. Trên đường tròn phụ, vẽ liên tiếp 6 dây, mỗi dây có độ dài 2R .Sau đó vẽ sáu đường tròn có tâm là mút của mỗi dây.
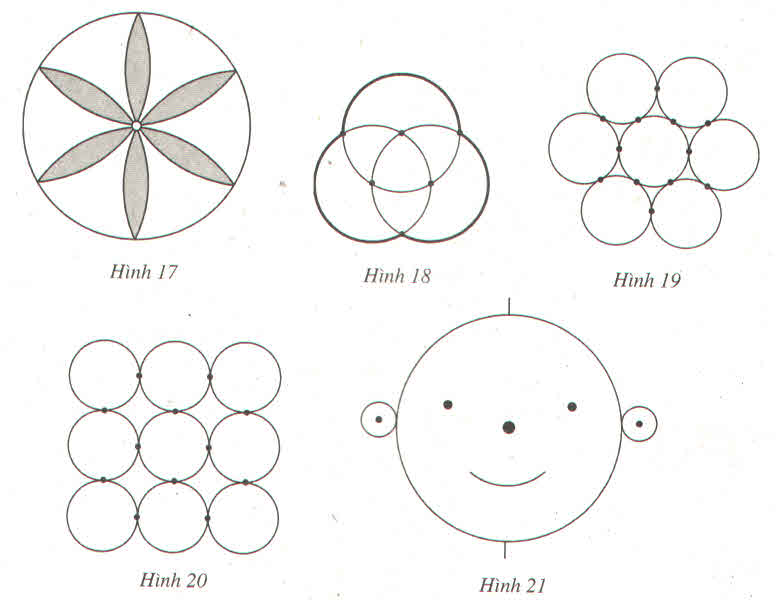
d) Vẽ đường tròn bán kính R bằng bán kình của đường tròn ở chính giữa. Vẽ liên tiếp sáu dây, mỗi dây dài R. Vẽ sáu nửa đường tròn ra phía ngoài của đường tròn vừa vẽ mỗi nửa đường tròn có đường kính là mỗi dây.
TT
18 tháng 4 2017
Sách Giáo Khoa
Cách vẽ:
Hình a) Trước hết vẽ đường tròn bán kính 1,2 cm rồi vẽ đường kính của đường tròn. Trên hai nửa mặt phẳng bờ đối nhau là đường kính vẽ hai nửa đường tròn có đường kính lần lượt là đoạn nối tâm tới một đầu của đường kính vừa vẽ. Sau cùng tô màu như hình vẽ.
Hình b) Trước hết, vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
Q
7 tháng 7 2017
3/ Chu vi hình chữ nhật:
\(\left(\dfrac{1}{4}+\dfrac{3}{10}\right)\cdot2=\dfrac{11}{10}\) (chưa biết đơn vị)
Diện tích hình chữ nhật:
\(\dfrac{1}{4}\cdot\dfrac{3}{10}=\dfrac{11}{20}\) (chưa biết đơn vị)
20 tháng 4 2017
Hop so be nhat la 4
Ta co: 2015=4+4+4+...+4+15 (500 so 4)
Vi 4 va 15 la hop so
Vay co tat ca 501 cach viet
Tick cho minh nhe
20 tháng 4 2017
Hợp số bé nhất là 4
> Ta có:2015=4+4+4+....+4+15( có tất cả 500 số 4)
Vì ta thấy 4 và 15 là hợp số
vậy nên suy ra ta sẽ có tất cả 501 cách viết
Tick mink nhé @Trịnh Minh Thành
3 tháng 7 2017
a) Để phân số \(\dfrac{12}{n}\) có giá trị nguyên thì :
\(12⋮n\)
\(\Leftrightarrow n\inƯ\left(12\right)\)
\(\Leftrightarrow n\in\left\{-1;1;-12;12;-2;2;-6;6;-3;3;-4;4\right\}\)
Vậy \(n\in\left\{-1;1;-12;12;-2;2-6;6;-3;3;-4;4\right\}\) là giá trị cần tìm
b) Để phân số \(\dfrac{15}{n-2}\) có giá trị nguyên thì :
\(15⋮n-2\)
\(\Leftrightarrow x-2\inƯ\left(15\right)\)
Tới đây tự lập bảng zồi làm típ!
c) Để phân số \(\dfrac{8}{n+1}\) có giá trị nguyên thì :
\(8⋮n+1\)
\(\Leftrightarrow n+1\inƯ\left(8\right)\)
Lập bảng rồi làm nhs!
24 tháng 4 2017
\(\left(x-2\right)\left(x-4\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2< 0\\x-4>0\end{matrix}\right.=>4< x< 2\left(1\right)\\\left\{{}\begin{matrix}x-2>0\\x-4< 0\end{matrix}\right.=>2< x< 4\left(2\right)}\end{matrix}\right.\)(1 ) vô lý=> loại
=> (x-2).(x-4)<0 <=> 2<x<4
b. ta có\(x^2+1>0\forall x\)
=>(x2 -1).(x2+1)<0 <=> (x2 -1)<0 <=> x2<1
<=> -1<x<1
câu c bạn làm tương tự
DD
1
26 tháng 7 2017
dấu hiệu chia hết cho 4 là : 2 số cuối cùng chia hết cho 4 thì số đó chia hết cho 4
dấu hiệu chia hết 5 : số có tận cùng là 0 ; 5 thì chia hết 5
Vì \(x1357y⋮5\) => y=0 hoặc 5
TH1 : y = 0
=> x13570\(⋮5\)
vì 70 \(⋮4̸\) ( loại )
TH2 : y = 5
=> \(x13575⋮5\) nhưng 75 ko chia hết 4 (loại )
từ 2 trường hợp trên => ko tồn tại y
\(\Leftrightarrow\) ko có số x1357y \(⋮5;4\)
DD
1
21 tháng 10 2017
Vì \(\overline{x1357y}⋮5\) nên \(y\in\left\{0;5\right\}\).
Do \(75⋮4\) nên \(y=0\). Ta được \(\overline{x13570}\).
Vì \(\overline{x13570}⋮4;5\) nên \(x\in\left\{1;2;3;4;5;6;7;8;9\right\}\).
Vậy \(x\in\left\{1;2;3;4;5;6;7;8;9\right\}\)và \(y=0\).
DT
Đỗ Thanh Hải
CTVVIP
3 tháng 3 2017
Đây bạn
Viết lại bài toán cần chứng minh
13+23+33+..n3=(1+2+3+...+n)213+23+33+..n3=(1+2+3+...+n)2
Với n=1;n=2n=1;n=2 thì đẳng thức hiển nhiên đúng, hay chính là câu a,b đó 
Giả sử đẳng thức đúng với n=kn=k
Tức 13+23+33+...k3=(1+2+3+4..+k)213+23+33+...k3=(1+2+3+4..+k)2
Ta sẽ chứng minh nó đúng với n=k+1n=k+1
Viết lại đẳng thức cần chứng minh 13+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)213+23+33+...k3+(k+1)3=(1+2+3+4..+k+k+1)2 (*)
Mặt khác ta có công thức tính tổng sau 1+2+3+4+...+n=n(n+1)21+2+3+4+...+n=n(n+1)2
⇒(1+2+3+4+...+n)2=(n2+n)24⇒(1+2+3+4+...+n)2=(n2+n)24
Vậy viết lại đẳng thức cần chứng minh
(k2+k)24+(k+1)3=(k2+3k+2)24(k2+k)24+(k+1)3=(k2+3k+2)24
⇔(k2+3k+2)2−(k2+k)2=4(k+1)3⇔(k2+3k+2)2−(k2+k)2=4(k+1)3
Bằng biện pháp "nhân tung tóe", đẳng thức cần chứng minh tuơng đuơng
⇔4k3+12k2+12k+4=4(k+1)3⇔4k3+12k2+12k+4=4(k+1)3
⇔4(k+1)3=4(k+1)3⇔4(k+1)3=4(k+1)3 ~ Đẳng thức này đúng.
Vậy theo nguyên lý quy nạp ta có đpcm.
3 tháng 3 2017
Giải hẳn hoi nha các bạn, đừng có viết luôn dạng tổng quát, nha 
a) Bước 1. Vẽ đường tròn (O,1cm) và đường tròn (O,2 cm).
Bước 2. Chia đường tròn (O;2crn) thành 6 cung bằng nhau bởi các điểm chia: O 1 , O 2 , O 3 , O 4 , O 5 , O 6
Bước 3. Vẽ 6 đường tròn tương ứng.
b) Bước 1. Vẽ hình vuông và hai đường chéo cắt nhau tại O.
Bước 2. Vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
Bước 3. Tô màu như hình vẽ.
c) Bước 1. Vẽ đường tròn (O;2cm) rồi chia đường tròn thành 6 cung bằng nhau bởi các điểm chia: O 1 , O 2 , O 3 , O 4 , O 5 , O 6
Bước 2. Lấy 6 điểm đó là tâm vẽ các cung tròn (chỉ vẽ các cung là giao của đường tròn thứ hai với đường tròn (O;2 cm).