SJ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
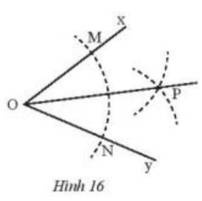
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
ND
2 tháng 6 2024
Cho đường tròn tâm O và đường tròn tâm O phẩy cắt nhau tại 2 điểm A và B Chứng minh O phẩy là tia phân giác của góc AOB
Vẽ hình nha ra các bạn!!!
18 tháng 11 2016
Xét tam giác OBC và tam giác OAC có:
OC: cạnh chung
OB = OA (vì cùng nằm trên 1 cung tròn tâm O)
BC = AC (vì cung tròn tâm A = cung tròn tâm B)
Vậy tam giác OBC = tam giác OAC (c.c.c)
=> góc COB = góc COA (2 góc tương ứng)
=> OC là phân giác của góc xOy (đpcm)
24 tháng 11 2017
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
OA=OB (vì cùng nằm trên cung tròn tâm O)
AC=BC (vì C là giao điểm của cung tròn tâm A và cung tròn tâm B)
OC là cạnh chung
\(\Rightarrow\Delta OAC=\Delta OBC\) (c.c.c)
\(\Rightarrow\widehat{AOC}=\widehat{BOC}\) (hai góc tương ứng) (1)
Vì điểm C nằm trong \(\widehat{xOy}\) nên tia OC nằm giữa 2 tia Ox và Oy (2)
Từ (1) và (2) suy ra tia OC là tia phân giác của \(\widehat{xOy}\) (đpcm)
11 tháng 11 2016
A B C D a)
ta có D là giao điểm của cung tròn tâm B với cung tròn tâm C=>BD là bán kính của cung tròn tâm B và CD là bán kính của cung tròn tâm C
ta có: DB là bán kính của cung tròn tâm B mà AC cũng là bán kính của cung tròn tâm B=> AC=BD
CM tương tự ta có: CD=AB
xét \(\Delta ABC\) và \(\Delta DCB\) có:
BD=AC(cmt)
AB=DC(cmt)
BC(chung)
\(\Rightarrow\Delta ABC=\Delta DCB\left(c.c.c\right)\)
=>\(\widehat{BAC}=\widehat{BDC}=80^o\)
b)
theo câu a, ta có:
\(\Delta ABC=\Delta DCB\Rightarrow\widehat{ABC}=\widehat{BCD}\)
=>CD//AB(2 góc slt)
11 tháng 11 2016
A B C D Nếu bạn xem ko đc hình thì xem hình này cũng được, khi nãy mk vẽ quên căn
ở câu a, mk ko quen cách diễn đạt lớp 9 cho lắm nên thông cảm nhé
làm thế nào ?