Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

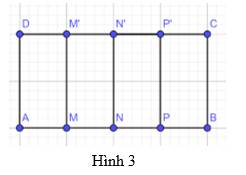
Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB.
Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN.
Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB.

a/ \(\Delta ABM\)và \(\Delta CDM\)có: AM = CM (M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(đối đỉnh)
BM = DM (gt)
=> \(\Delta ABM\)= \(\Delta CDM\)(c. g. c)
b) Ta có \(\Delta ABM\)= \(\Delta CDM\)(cm câu a) => \(\widehat{BAC}=\widehat{ACD}\)(hai góc tương ứng bằng nhau ở vị trí so le trong)
=> AB // CD (đpcm)

a) Xét ∆AMB và ∆AMC có :
BM = MC ( M là trung điểm BC )
AM chung
AB = AC
=> ∆AMB = ∆AMC (c.c.c)
b) Vì AB = AC
=> ∆ABC cân tại A
Mà AM là trung tuyến
=> AM \(\perp\)BC
Mà a\(\perp\)AM
=> a//BC ( từ vuông góc tới song song )
c) Vì CN//AM (gt)
AN//MC ( a//BC , M thuộc BC)
=> ANCM là hình bình hành
=> NC = AM , AN = MC
Mà AMC = 90°
=> ANCM là hình chữ nhật
=> NAM = AMC = MCN = CNA = 90°
Xét ∆ vuông NAC và ∆ vuông MCA có :
AN = MC
AM = CN
=> ∆NAC = ∆MCA (ch-cgv)
d) Vì ANCM là hình chữ nhật (cmt)
=> AC = MN , I là trung điểm 2 đường chéo NM và AC (dpcm)

a: Xét ΔANB và ΔANC có
AN chung
NB=NC
AB=AC
Do đó: ΔANB=ΔANC

a) Ta có MN vuông góc với AB ( do MN là đường trung trực của đoạn thẳng AB theo giả thuyết nên suy ra)
và đường thẳng m cũng vuông góc với đoạn thẳng AB ( theo giả thiết)
nên từ đó ta suy ra MN//m (đpcm)
b) Từ MN//m ta suy ra MIC=ICB (hai góc so le trong)
mà ICB= 60 độ => MIC=60 độ
c) Ta có HIB= HIN+NIB
Mặt khác HIN=MIC=60 độ ( so le trong)
và NIB=90 độ (gt)
suy ra HIB= 60+90=150 độ
d) Vì theo giả thiết ta có đường thẳng a đi qua C và song song với MN và điểm C lại nằm trên cùng một đường thẳng m với điểm B mà đường thẳng m lại song song với đường thẳng MN nên suy ra đường thẳng a trùng với đường thẳng m và đi qua B

ABCMabNI
a)Xét \(\Delta\)AMB và \(\Delta\)AMC
AB=AC(GT)
MB=MC(GT)
AM là cạnh chung
=>\(\Delta\)AMB=\(\Delta\)AMC
b)Ta có:\(\Delta\)AMB=\(\Delta\)AMC=>góc AMC=góc AMB=\(^{90^0}\)
=>AM\(\perp\)BC
Ta lại có:góc aAM=\(90^0\);góc AMB=\(90^0\)mà hai góc này nằm ở vị trí so le trong
=>a//BC
c)Xét \(\Delta\)AMC và \(\Delta\)CNA
AC là cạnh chung
a//BC=>góc MCA=góc NAC(hai góc so le trong)
b//AM=>góc MAC=góc ACN(hai góc so le trong)
=>\(\Delta\)AMC=\(\Delta\)CNA
d)Xét\(\Delta\)INC và\(\Delta\)IMA
góc NIC=góc AIM(đối đỉnh)
IC=IA(GT)
góc ACN=góc MAC(câu c)
=>\(\Delta\)INC=\(\Delta\)IMA
=>IN=IM
=>I là trung điểm của MN
Hk tốt ^-^
a và b) Xét ΔAMBΔAMB và ΔAMCΔAMC có:
AMAM: chung
MB=MC(gt)MB=MC(gt)
AB=AC(gt)AB=AC(gt)
Vậy ΔAMB=ΔAMC(c.c.c)ΔAMB=ΔAMC(c.c.c)
⇒AMBˆ=AMCˆ⇒AMB^=AMC^
Mà AMBˆ+AMCˆ=180oAMB^+AMC^=180o
Nên AMBˆ=AMCˆ=AMB^=AMC^=180o2=90o180o2=90o
⇒AM⊥BC⇒AM⊥BC
Ta có a//BCa//BC vì cùng vuông góc với AMAM
c) Xét tứ giác ANCMANCM có:
Aˆ=Mˆ=90oCˆ=AMCˆ=90o(b//AM)A^=M^=90oC^=AMC^=90o(b//AM)
Nên ANCMANCM là hình chữ nhật ⇒{AM=NCAN=MC⇒{AM=NCAN=MC
Xét ΔAMCΔAMC và ΔCNAΔCNA có: ⎧⎩⎨⎪⎪AM=NCAMCˆ=ANCˆ=90oAN=MC{AM=NCAMC^=ANC^=90oAN=MC
Nên ΔAMCΔAMC==ΔCNAΔCNA(c.g.c)(c.g.c)
d) II là trung điểm ACAC ⇒I⇒I là giao 2 đường chéo của hình chữ nhật
⇒I⇒I là trung điểm MN
AI TRẢ LỜI MIK K LUÔN Ạ TẠI TỐI MIK PHẢI NỘP CHO CÔ RỒI 😭
K* đó mấy bạn ưi :<